本文章是 Udemy 課程 《機器學習 A-Z》 的學習筆記。不同於以往的筆記,本文將用一整篇文章來記錄整個課程的內容,因此本文會非常非常非常長。如果你需要找到某個特定的內容,歡迎使用目錄來進行檢索。
資料預處理
引入標準庫
import numpy as npimport matplotlib.pyplot as pltimport pandas as pd匯入資料集
dataset = pd.read_csv('Data.csv')我們需要創建一個包含自變量的 matrix,以及一個包含因變量的 vector。
# iloc 是一個函數,用來取得資料集中的特定部分# [] 中,第一個“:”表示我們要取得所有的列,第二個“:-1”表示我們要取得除了最後一欄的所有的欄# .values 表示我們要取得這個部分的值X = dataset.iloc[:, :-1].valuesY = dataset.ionic[:, 3].values資料缺損時的解決方法
解決方案1:刪除有缺損的資料。比較簡單,但風險較大。
解決方案2:用平均值填補缺損的資料。比較保險,但可能會導致資料集的平均值偏移。
我們使用 scikit-learn 中的 Imputer 類來解決這個問題。
from sklearn.impute import SimpleImputerimputer = SimpleImputer(missing_values=np.nan, strategy='mean') # missing_values 表示缺失值的標記,strategy 表示填補策略,這裡使用平均值imputer = imputer.fit(X[:, 1:3]) # 這裡只對包含缺失值的列進行填補X[:, 1:3] = imputer.transform(X[:, 1:3]) # 將填補好的資料放回原來的資料集這裡需要注意,在 scikit-learn 0.20 版本中,
Imputer已經被棄用,取而代之的是SimpleImputer型別。與影片中不同的部分,以本文為準。
分類資料的處理
所謂的分類資料,就是指資料集中的某些欄位是類別型的,而不是數值型的。比如說,國家、性別、是否等等。這些資料無法直接用於機器學習模型的訓練,因此我們需要對這些資料進行處理。
這類資料的處理,通常是將其轉換為數值型資料。比如說,我們可以將國家轉換為 0、1、2 等數字,性別轉換為 0、1 等數字。這樣,這些資料就可以被機器學習模型所接受。
我們使用 scikit-learn 中的 LabelEncoder 類來解決這個問題。
from sklearn.preprocessing import LabelEncoder
labelencoder_X = LabelEncoder()X[:, 0] = labelencoder_X.fit_transform(X[:, 0]) # 對第一列進行轉換好,我們又有了一個問題,這樣的轉換會讓機器學習模型認為這些數字之間存在大小關係,比如說,0 < 1 < 2。這樣的轉換是不合理的,因為這些數字只是用來表示不同的類別,並不存在大小關係。
這就是我們接下來要進行的處理,我們需要使用到虛擬編碼。比如,我們將國家由一列轉換為三列,每一列代表一個國家,如果這一列的資料是這個國家,則為 1,否則為 0。
我們需要的工具是 OneHotEncoder。
from sklearn.preprocessing import OneHotEncoderfrom sklearn.compose import ColumnTransformer
ct = ColumnTransformer( transformers=[('encoder', OneHotEncoder(), [0])], # 這裡的 0 表示我們要對第一列進行虛擬編碼,'encoder' 是一個標記,可以隨意取名 remainder='passthrough' # 這裡表示我們保留其他列的資料)
X = np.array(ct.fit_transform(X), dtype=np.float)需要注意,當前版本的 sklearn,需要用到
ColumnTransformer配合OneHotEncoder()來做。
這樣我們就完成了對分類資料的處理。
將資料集分為訓練集和測試集
為什麼要將資料集分為訓練集和測試集?什麼是訓練集?什麼是測試集?
我們首先需要理解機器學習的過程。機器學習的目的是透過訓練集來訓練模型,然後透過測試集來測試模型的性能。因此我們的訓練集就相當於學習的過程,而測試集就相當於考試的過程。
我們在 Python 實現這個過程:
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0) # test_size 表示測試集的比例,random_state 是一個隨機種子,可以確保每次運行的結果一致。其中,test_size 建議不超過 0.3擬合和過擬合:擬合是指模型訓練的過程,過擬合是指模型在訓練集上表現很好,但在測試集上表現很差。這是一個很常見的問題,我們需要透過調整模型的參數來解決這個問題。
特徵縮放
經典問題:是什麼?為什麼?
特徵縮放是指將所有的特徵都縮放到同一個範圍。為什麼要這麼做?因為機器學習模型是基於歐式距離來計算的,如果特徵的範圍不同,那麼模型就會偏向於範圍較大的特徵。這樣就會導致模型的性能下降。
通俗一點來講,就是如果我們有兩個特徵,一個特徵的範圍是 0 到 1,另一個特徵的範圍是 1 到 1000,那麼模型就會偏向於第二個特徵。這樣的結果是不合理的,因為兩個特徵應該是同等重要的。比如,年齡的範圍是 0 到 100,而收入的範圍是 0 到 100000,這樣的範圍差異就很大。
我們有兩個方法來進行特徵縮放:標準化和歸一化。
- 標準化公式是:,其中 是平均值, 是標準差。
- 歸一化公式是:。
我們使用 scikit-learn 中的 StandardScaler 來進行標準化。
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()X_train = sc_X.fit_transform(X_train) # 這裡需要 fit 和 transform,因為我們需要計算平均值和標準差X_test = sc_X.transform(X_test) # 這裡只需要 transform,不需要 fit,因為我們已經在訓練集上 fit 過了我們是否需要對因變量進行特徵縮放呢?這取決於具體的問題。在某些情況下,我們需要對因變量進行特徵縮放,比如說,當因變量的範圍很廣時。但在大多數情況下,我們不需要對因變量進行特徵縮放。
回歸
簡單線性回歸
我們首先舉一個可以應用簡單線性回歸的例子。假設我們有一個資料集,其中包含了員工的工資和工作年限。我們想要透過工作年齡來預測員工的工資。
簡單線性回歸中,一般會有兩個問題。第一個問題是,我們需要找到自變數和應變數之間的關係。第二個問題是,使用這個關係來預測新的資料。
我們來回顧一下簡單線性回歸的公式:,其中 是應變數, 是自變數, 是截距, 是斜率。
我們來看一下在一個二維的平面上是如何標示的。
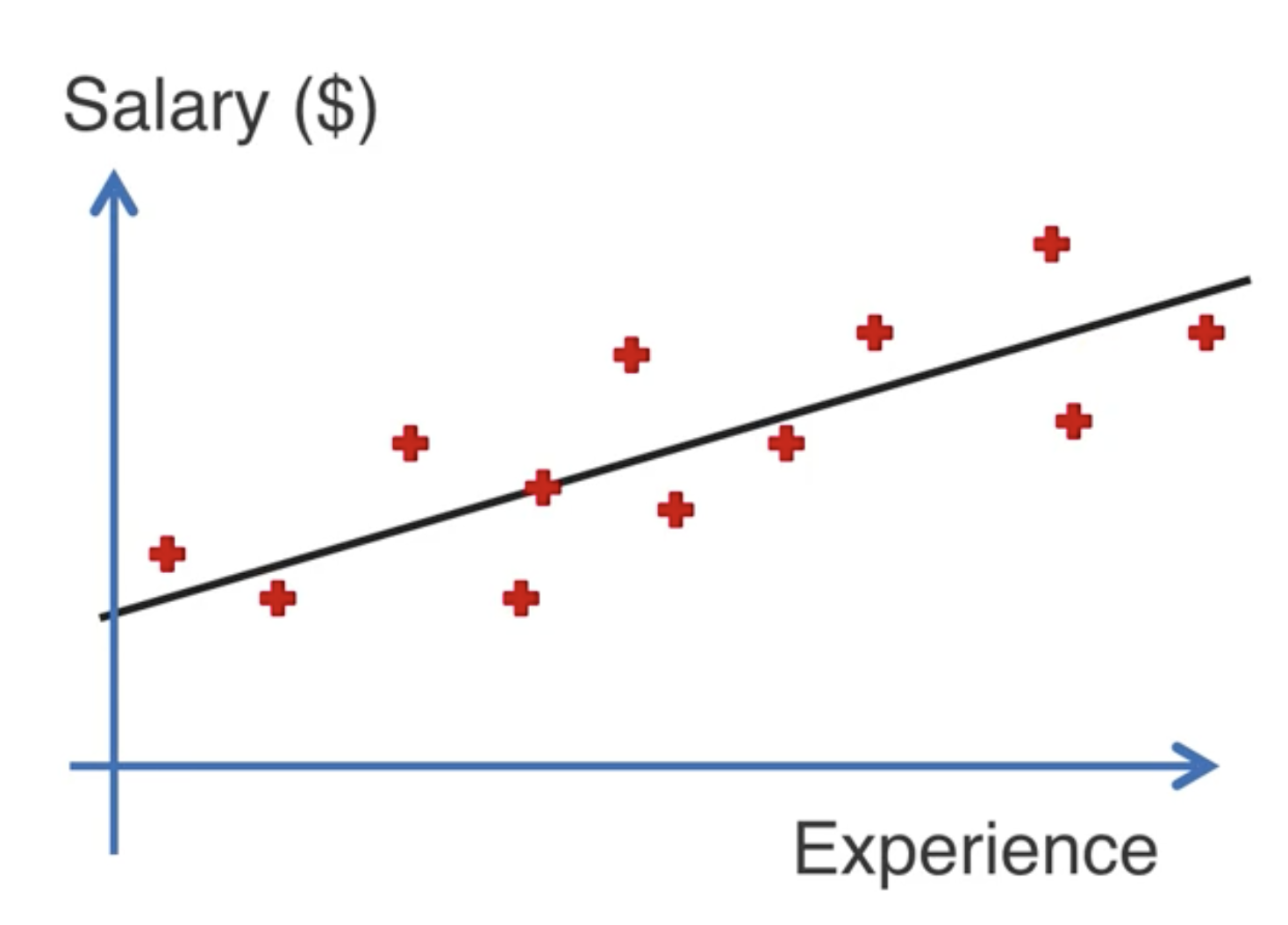
我們將上面的例子展示到二維平面中,其中 x 軸是工作年限,y 軸是工資。我們可以看到,這些點大致上是在一條直線上的。這條直線即可用 來表示。我們的目標就是要找到這條直線,即找到 和 。
這個過程叫做擬合,擬合的過程可以用一個嚴謹的數學過程來找到。
這個過程可以這樣來通俗描述:計算 的最小值。其中, 是真實值, 是預測值。這個過程叫做最小二乘法。
接下來,我們在 Python 中利用簡單線性回歸對我們的資料集進行擬合。
from sklearn.linear_model import LinearRegression
# 機器regressor = LinearRegression()
# 學習regressor.fit(X_train, Y_train) # 這裡是擬合的過程,我們將訓練集的自變數和應變數傳入模型中
# 預測Y_pred = regressor.predict(X_test) # 這裡是預測的過程,我們將測試集的自變數傳入模型中,得到預測值我們可以透過視覺化來看一下我們的模型是如何擬合的。
plt.scatter(X_train, Y_train, color='red') # 這裡是畫出訓練集的散點圖
plt.plot(X_train, regressor.predict(X_train), color='blue') # 這裡是畫出擬合的直線
plt.title('Salary vs Experience (Training set)') # 這裡是設置標題
plt.xlabel('Years of Experience') # 這裡是設置 x 軸的標籤
plt.ylabel('Salary') # 這裡是設置 y 軸的標籤
plt.show() # 這裡是顯示圖像得到的圖片如下:
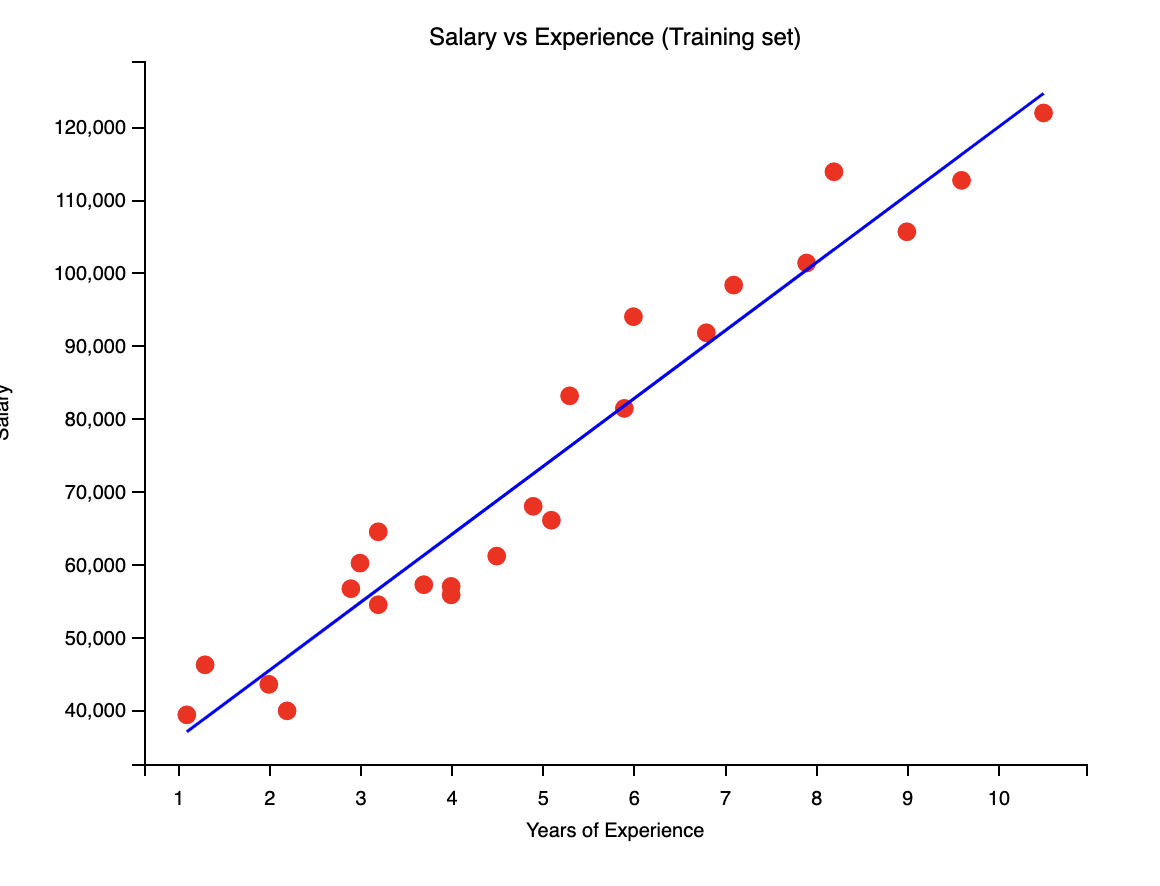
你也可以將測試集的資料畫出來,看看模型是如何預測的。
多元線性回歸
我們之前所講的簡單線性回歸,適用於只有一個自變數的情況。但在現實生活中,我們往往有多個自變數。這時,我們就需要使用多元線性回歸。
多元線性回歸的公式是:。我們的任務就是找到 。
多元線性回歸的應用條件如下:
- Linearity 線性
- Homoscedasticity 同變異數
- Multivariate normality 多變數常態性
- Independence of errors 誤差獨立
- Lack of multicollinearity 無多重共線性
虛擬變數和虛擬變數的陷阱。當我們有一個分類變數時,我們需要將其轉換為虛擬變數。比如說,我們有一個國家變數,我們需要將其轉換為虛擬變數。但是,我們不能將所有的虛擬變數都放入模型中,這樣會導致虛擬變數陷阱。我們剛剛有講過,應用多元線性回歸的條件之一是無多重共線性,即其中一個自變數不應該同其他自變數有明顯的線性關係。而虛擬變數陷阱就是一種多重共線性。
接下來,我們來看一看如何來建立一個多元線性回歸模型。這個過程可能沒有說起來那樣簡單。
首先一步就是選擇自變數,看看到底有哪些自變數適合放到模型中,哪些不適合。這個過程叫做特徵選擇。
有幾種方法來構建我的模型:
- All in:將所有的自變數都放入模型中。
- Backward Elimination:反向選擇。這是一種逐步回歸的方法,我們首先將所有的自變數放入模型中,然後逐步刪除那些不顯著的自變數。
- Forward Selection:正向選擇。這是一種逐步回歸的方法,我們首先將一個自變數放入模型中,然後逐步添加那些顯著的自變數。
- Bidirectional Elimination:雙向選擇。這是一種結合了反向選擇和正向選擇的方法。
- Score Comparison:分數比較。這是一種基於信息準則的方法,比如 AIC 和 BIC。
我們分別來看。
All in
這是一種最簡單的方法,就是將所有的自變數都放入模型中。這種方法的好處是簡單。應用於如果所有自變數都是重要的,那麼這種方法是最好的。且 All in 可以為 Backward Elimination 提供一個很好的初始點。
Backward Elimination
這是一種逐步回歸的方法,我們首先將所有的自變數放入模型中,然後逐步刪除那些不顯著的自變數。這種方法的好處是可以節省時間,因為我們不需要一個一個地添加自變數。但是,這種方法也有一個缺點,就是可能會刪除一些重要的自變數。
步驟如下:
- 選擇一個顯著水平,比如說 0.05。
- 將所有的自變數放入模型中,得到擬合好的模型。
- 找到模型中 p 值最大的自變數,如果 p 值大於顯著水平,則刪除這個自變數。
- 重新擬合模型,重複步驟 3,直到所有的自變數的 p 值都小於顯著水平。
Forward Selection
這是一種逐步回歸的方法,我們首先將一個自變數放入模型中,然後逐步添加那些顯著的自變數。這種方法的好處是可以節省時間,因為我們不需要一個一個地添加自變數。但是,這種方法也有一個缺點,就是可能會添加一些不重要的自變數。
步驟如下:
- 選擇一個顯著水平,比如說 0.05。
- (對每一個 應用簡單線性回歸),計算 p 值。找到最小的 p 值。
- 如果 p 值小於顯著水平,則將這個自變數添加到模型中並進行重新擬合。
- 使用新模型,繼續重複步驟 2 和 3,直到所有 p 值小於顯著水平的自變數都被添加入模型。
Bidirectional Elimination
這是一種結合了反向選擇和正向選擇的方法。
步驟如下:
- 選擇兩個顯著水平。一個代表添加自變數,一個代表刪除自變數。比如 SLENTER = 0.05,SLSTAY = 0.05。
- 執行 Forward Selection,來決定是否採納一個新的變數。(new variables must have p-value < SLENTER to enter)
- 執行 Backward Elimination 的全過程,可能要剔除舊的變數。(old variables must have p-value < SLSTAY to stay)
- 重複步驟 2 和 3,直到所有變數都符合標準。
Score Comparison
這是一種基於信息準則的方法,比如 AIC 和 BIC。這是一種對模型打分的方法,我們可以透過這種方法來選擇最好的模型。有 n 個自變數的模型共有 種組合,這種方法可以幫助我們找到最好的模型。缺點是計算量大。
實戰
我們來實戰。
假設我們作為一家資本風投公司的首席資料官,我們有一個資料集,其中包含了一些公司的研發支出、行銷支出、管理支出、坐落位置。我們想要透過這些支出來預測公司的利潤。
我們在 Python 中用反向淘汰來實現這個過程。
from sklearn.linear_model import LinearRegression
# 創建回歸器regressor = LinearRegression()
# 擬合(all in)regressor.fit(X_train, Y_train)
# 預測y_pred = regressor.predict(X_test)接下來,我們使用反向淘汰算法來更新模型。在此之前,我們需要對資料進行一下處理。
在之前我們引入的 sklearn.linear_model.LinearRegression 標準庫中,公式 中的 這一常數項已經被考慮在內了。但是在我們之後要使用的標準庫中,則不包含該常數。因此,我們需要為原始資料加入一欄都為 1 的變數。
X_train = np.append(arr=np.ones((40, 1)).astype(int), values=X_train, axis=1)然後我們來看一下反向淘汰的過程。
import statsmodels.api as sm
# 創建一個新的矩陣,包含所有的自變數X_opt = X_train[:, [0, 1, 2, 3, 4, 5]]
# 創建一個新的回歸器regressor_OLS = sm.OLS(endog=Y_train, exog=X_opt).fit()
# 檢查 p 值print(regressor_OLS.summary())而後我們會得到如下輸出:
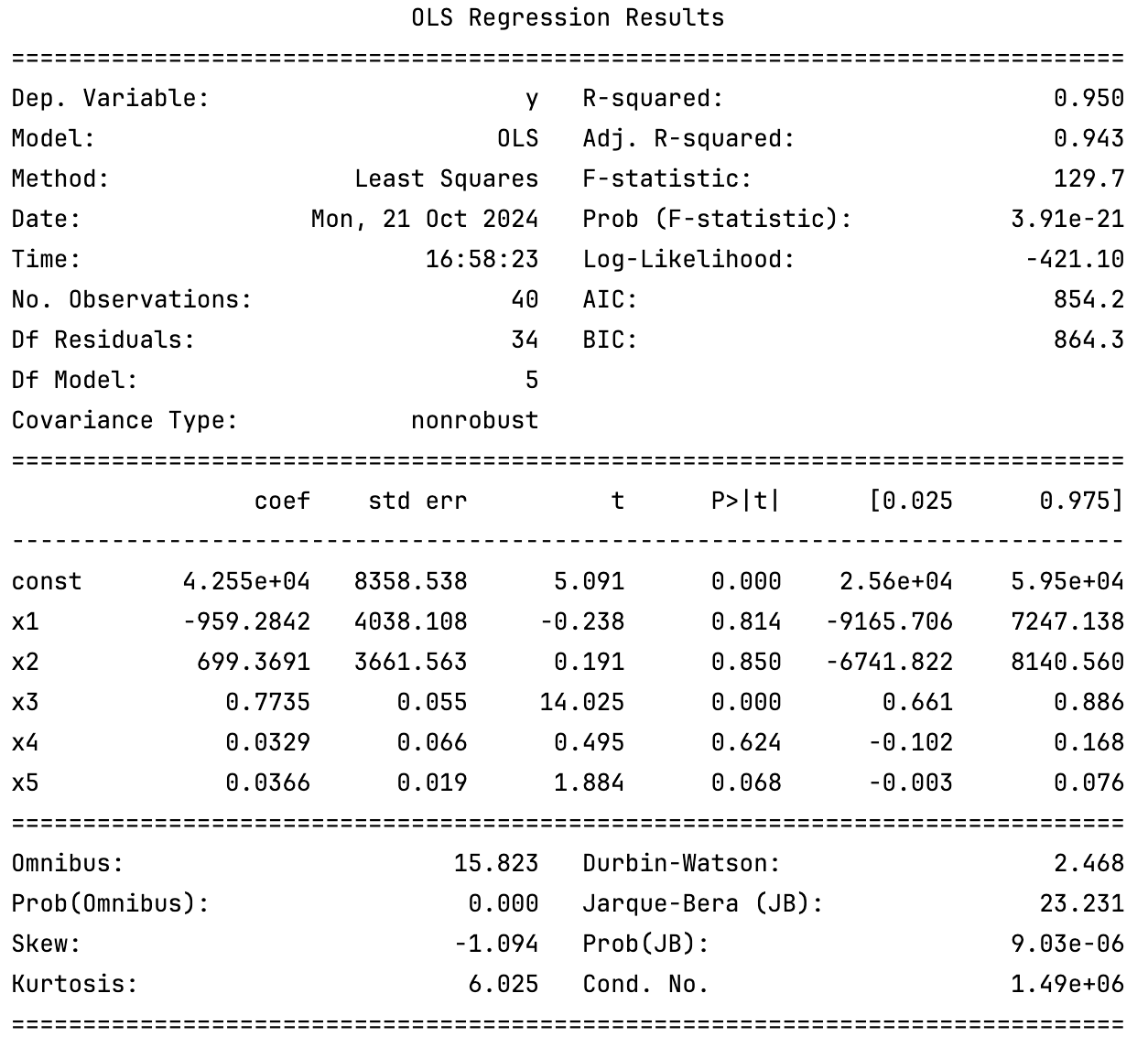
我們所需要的 p-value 即為 P>|t| 欄位。如果自變數的最大 p-value 大於 0.05,則我們可以將其刪除。
比如,上述過程暴露的結果是,x2 的 p-value 為 0.850,大於 0.05,因此我們可以將其刪除。
X_opt = X_train[:, [0, 1, 3, 4, 5]]重複這個過程,直到所有的自變數的 p-value 都小於 0.05。
多項式回歸
多項式回歸是一種特殊的線性回歸,其中自變數和應變數之間的關係不是線性的,而是多項式的。比如,。多項式線性回歸中,只有一個自變數,而不是多元線性回歸中的多個自變數。
接下來我們來在 Python 中實現多項式回歸。
from sklearn.preprocessing import PolynomialFeatures
# 創建多項式特徵poly_reg = PolynomialFeatures(degree=4) # 這裡的 degree 表示多項式的最高次數
# 將自變數轉換為多項式X_poly = poly_reg.fit_transform(X_train) # 這裡將自變數 matrix 轉換為多項式 matrix
# 創建回歸器regressor = LinearRegression()
# 擬合regressor.fit(X_poly, Y_train)
# 預測y_pred = regressor.predict(poly_reg.fit_transform(X_test))我們還可以使用 plt 來視覺化我們的模型。並且根據圖像直觀看到模型的擬合效果。並且根據效果,可以調整多項式的次數。
評估回歸模型
R-squared:適用於一元線性回歸
公式即為:。其中 是殘差平方和, 是總平方和。
其中,,
的範圍是 0 到 1,越接近 1,表示模型越好。
Adjusted R-squared:適用於多元線性回歸
公式為:。其中 是樣本數, 是自變數的數量。
為什麼要有 Adjusted R-squared?因為 R-squared 會隨著自變數的增加而增加,即使這些自變數對模型沒有幫助。Adjusted R-squared 考慮了自變數的數量,因此對於多元線性回歸比 R-squared 更準確。
利用 Adjusted R-squared 在 Python 中來評估模型
假設在多項式回歸中,我們使用反向淘汰算法進行特徵選擇,由於 p-value 的限制,我們最終得到了一個模型。但是 p-value = 0.05 這個值是一個經驗值,並不是一個絕對的值。因此,當到最後,假設有一個變數的 p-value = 0.051,這個變數仍然被刪除,這是不合理的。因此,我們需要使用 Adjusted R-squared 來評估模型,再來決定是否需要去除這個變數。
import statsmodels.api as sm
# 創建一個新的矩陣,包含所有的自變數X_opt = X_train[:, [0, 1, 2, 3, 4, 5]]
# 創建一個新的回歸器regressor_OLS = sm.OLS(endog=Y_train, exog=X_opt).fit()
# 檢查 p 值print(regressor_OLS.summary())事實上,regressor_OLS.summary()這個函式會返回一個表格,其中包含了所有的統計信息,包括 p-value 和 Adjusted R-squared。比如上面那張:

我們可以看到,Adj. R-squared 就是 Adjusted R-squared。
分類
邏輯回歸
邏輯回歸是一種分類算法,用於將樣本分類為兩個或多個類別。邏輯回歸的目標是找到一個邏輯函數,將自變數映射到一個或多個類別。
首先我們需要理解分類問題。分類問題是一種監督學習問題,其中我們需要將樣本分類為兩個或多個類別。比如,我們有一個資料集,其中包含了一些患者的患病與否和年齡,我們想要透過年齡來預測患病與否。“患病與否”並非一個連續的變量,而是一個類別變量,只有“患病”和“不患病”兩種,因此這是一個分類問題。
接下來我們來認識 sigmod 函數。sigmod 函數是一種 S 型函數,其公式為:。其中 是概率, 是線性組合。則 ,而後我們可以得到 。如果我們畫出這個函數,我們可以看到這是一個 S 型函數,這就是 sigmod 函數。這個函數自變數是原來的自變數,應變數是假設為真的概率。
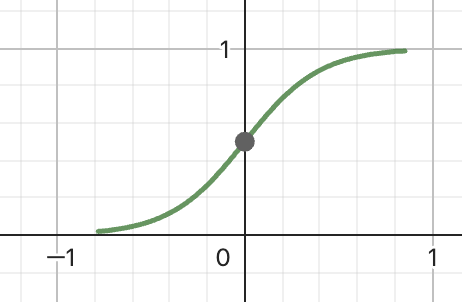
而後,我們使用這個模型來預測新的資料。如果 ,則我們預測為真,否則為假。這個過程即為邏輯回歸將自變數映射到類別的過程。
接下來我們來看一下在 Python 中如何實現邏輯回歸。
from sklearn.linear_model import LogisticRegression
# 創建回歸器classifier = LogisticRegression(random_state=0) # 這裡的 random_state 是一個隨機種子,可以確保每次運行的結果一致
# 擬合classifier.fit(X_train, Y_train)
# 預測Y_pred = classifier.predict(X_test)我們可以使用混淆矩陣來評估模型的性能。
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(Y_test, Y_pred)輸出的混淆矩陣可能如下:
[[65 3] [ 8 24]]其中,65 表示真陽性,3 表示假陽性,8 表示假陰性,24 表示真陰性。
使用視覺化來看一下模型的性能。
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, Y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)): plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('orange', 'blue'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('Age')plt.ylabel('Estimated Salary')
plt.legend()
plt.show()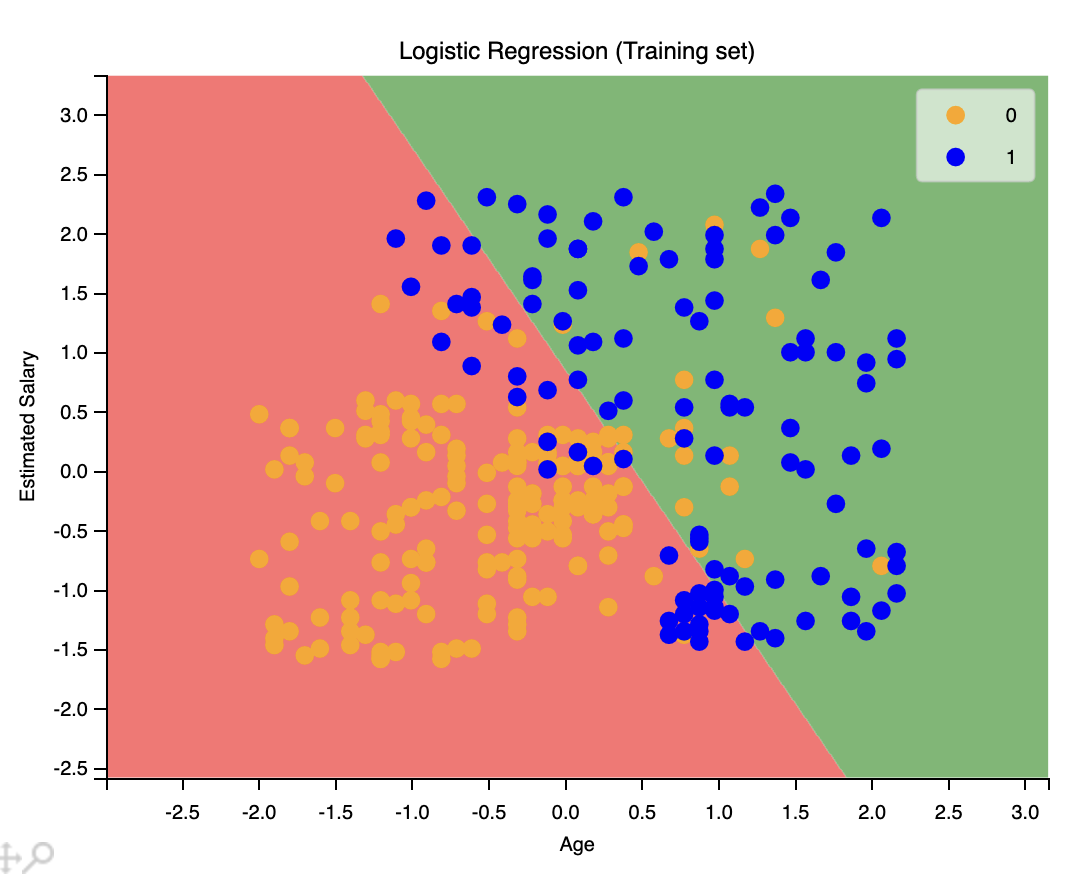
我們還可以使用之來匯出測試集的圖像。
X_set, y_set = X_test, Y_test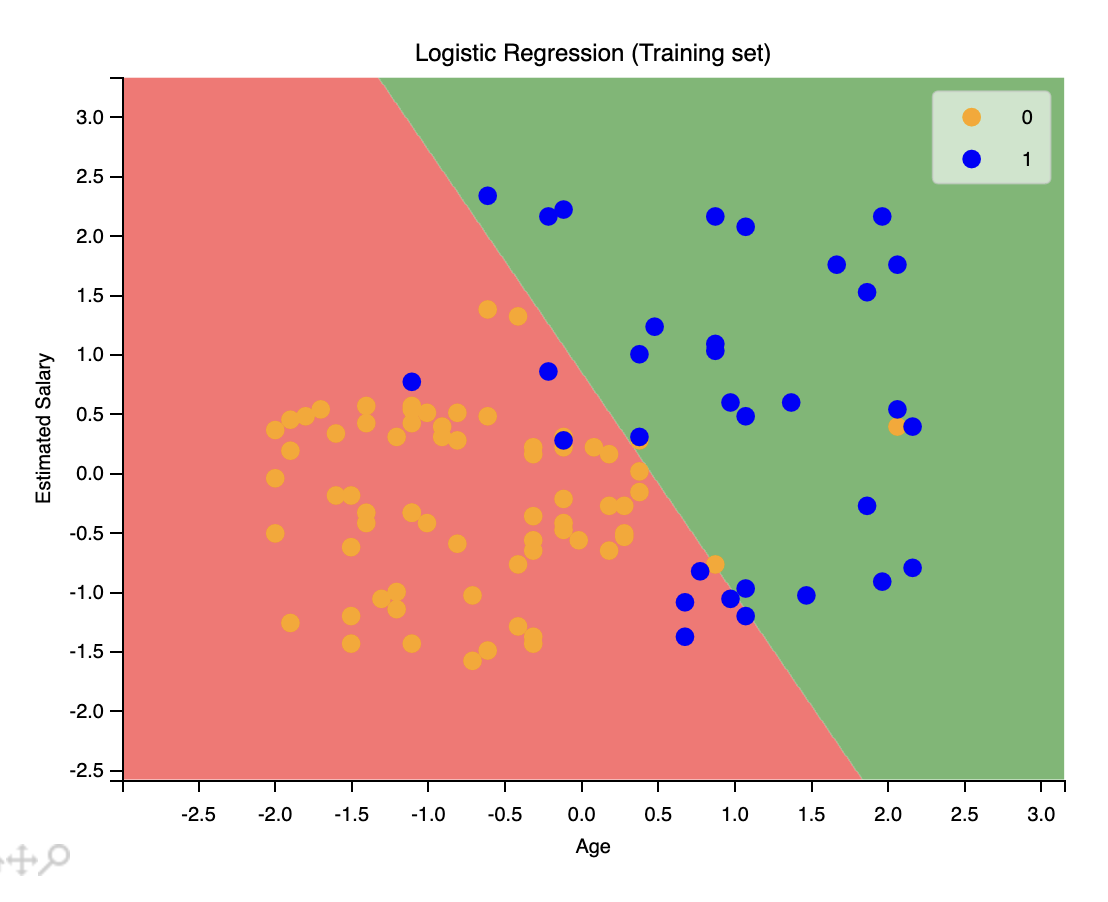
還記得我們之前提到的混淆矩陣嗎?輸出如下:
[[65 3] [ 8 24]]數一數,65 是圖像上紅色區域的橙色點的數量,24 是圖像上綠色區域的藍色點的數量。8 是圖像上紅色區域的藍色點的數量,3 是圖像上綠色區域的橙色點的數量。這就是混淆矩陣。直觀清楚了。
支援向量機 SVM
我們先來看這樣一個問題:
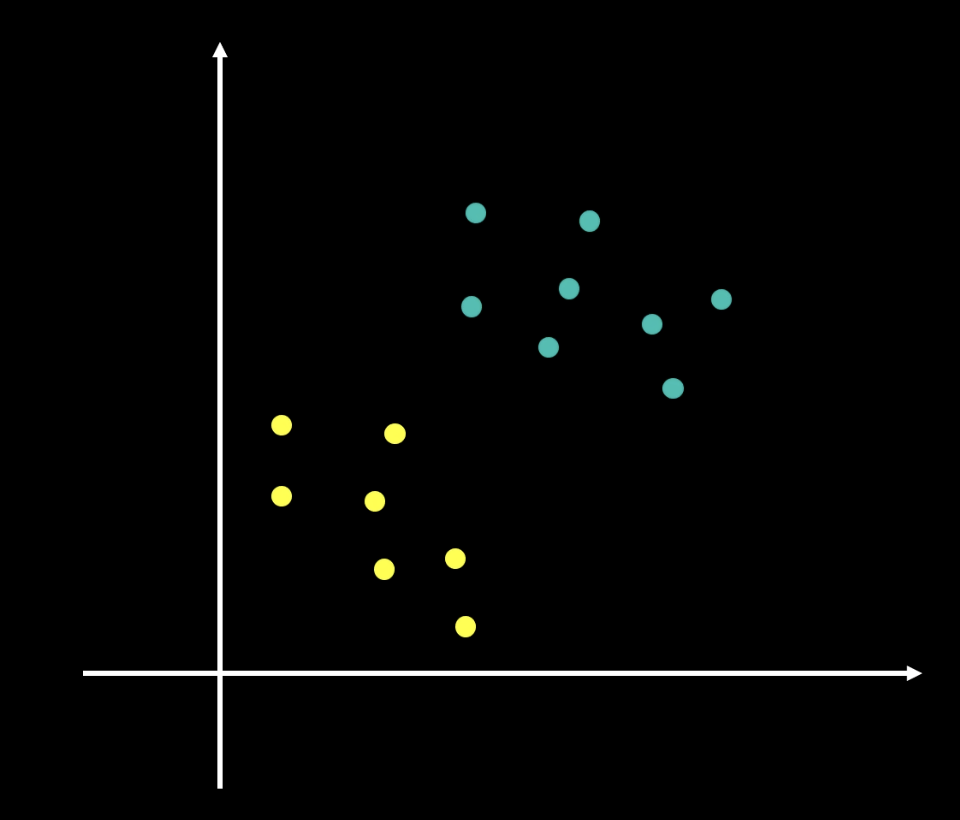
在如上一個二維平面中,我們有兩個類別,黃色和青色。我們的目標是找到一個最佳的分割線,將這兩個類別分開。並且對於之後加入的資料,也能夠根據這個分割線來正確分類。
由此可以延伸到高維度空間。比如說,我們有一個三維空間,我們的目標是找到一個最佳的平面,將這兩個類別分開。
支援向量機(SVM)就是一種用於分類的機器學習算法。SVM 的目標是找到一個最佳的分割超平面,將兩個類別分開。這個分割超平面是一個線性的超平面,即 。其中 是法向量, 是截距。
上面的問題中,對比以下兩張圖片,我們從直覺上不難看出,第二張圖片的分割線更好。在第一條分隔線中,如果有一筆新加的資料,那麼被分類錯誤的概率是很大的。但是在第二條分隔線中,由於兩類資料的所有點都離分隔線有一定距離,因此被分類錯誤的概率是很小的。
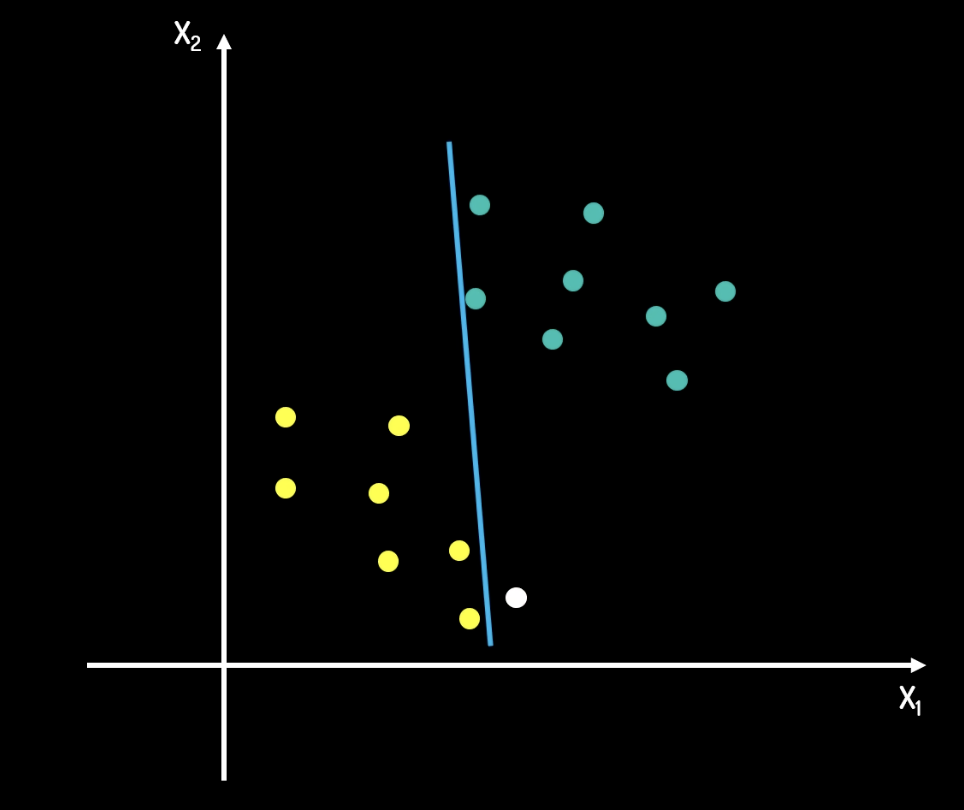
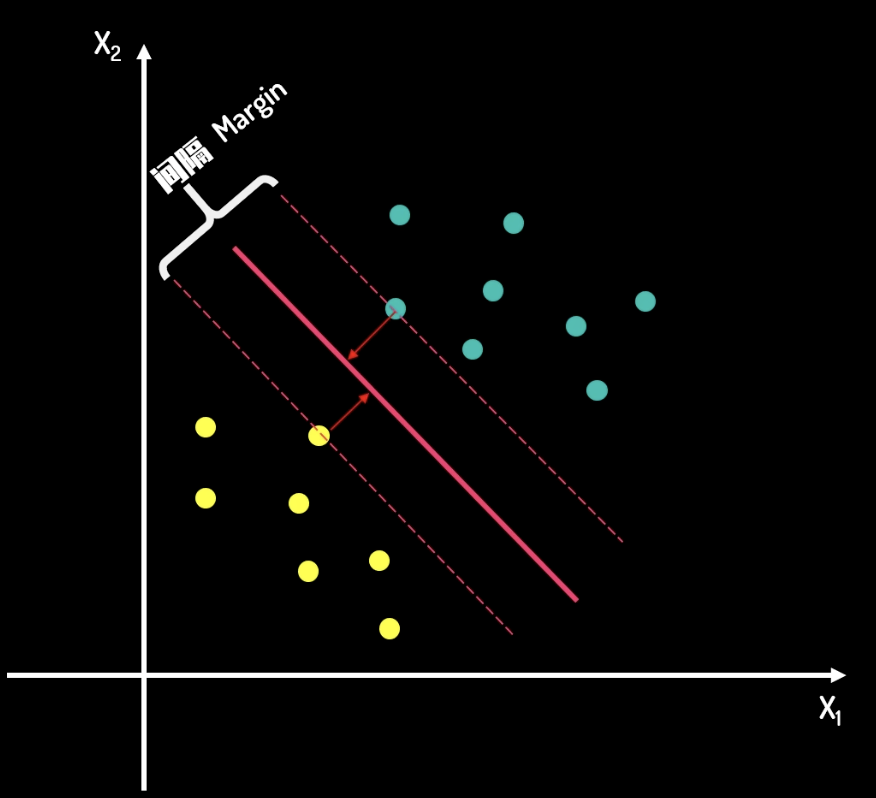
因此,支援向量機問題可以轉化為一個求取最大 margin 的問題。這條最大的 margin 中心,即為分割線。
分隔線的方程是 ,其中 是法向量, 是截距。而 margin 的方程是 和 。邊界所經過的點,即為支援向量。
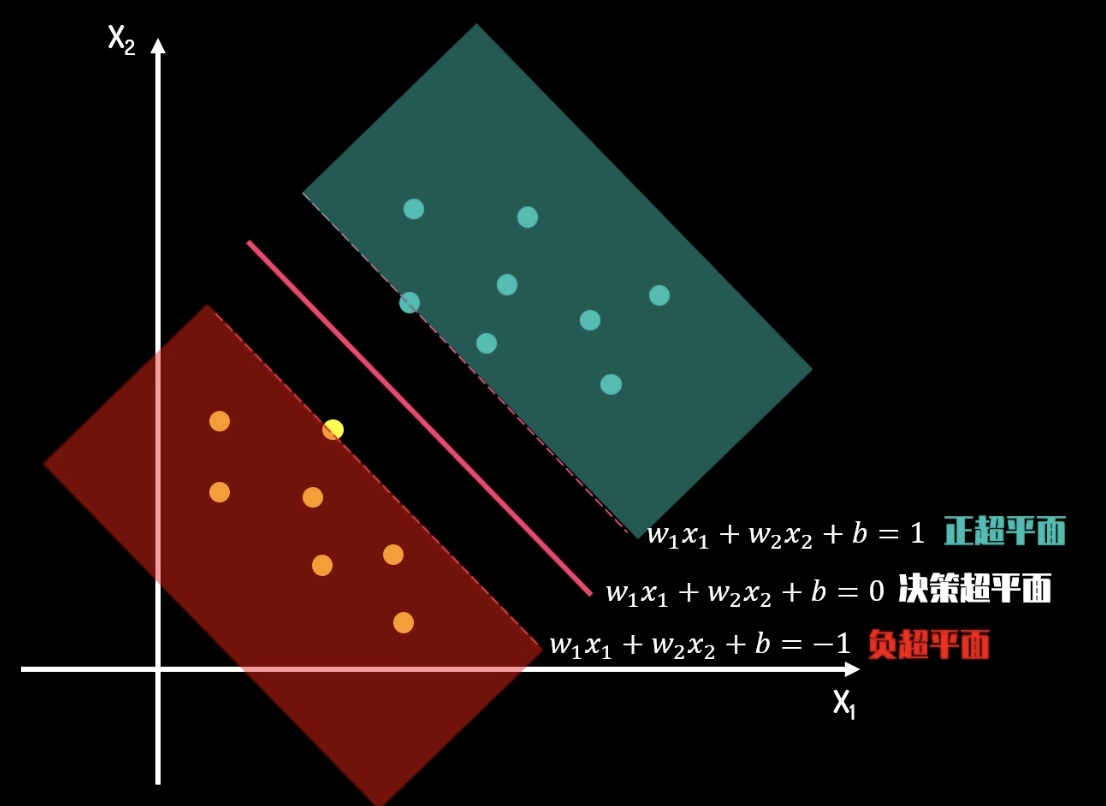
當然,我們的資料並不總是正常的,可能總會有一些離群值。這時,我們可以使用軟邊界。軟邊界允許一些點落在邊界內。每一個離群值都有一個“損失值”,我們可以把損失值看做我們的經營成本,而把 margin 看做我們的收益。我們的目標就是最大化收益,同時最小化成本。
我們在 Python 中實現這個過程。
from sklearn.svm import SVC
# 創建分類器classifier = SVC(kernel='linear', random_state=0)
# 擬合classifier.fit(X_train, Y_train)
# 預測Y_pred = classifier.predict(X_test)核函數支援向量機 Kernel SVM
在實際應用中,我們的資料可能不是線性可分的。這時,我們可以使用核函數支援向量機(Kernel SVM)。比如說下面的這種:
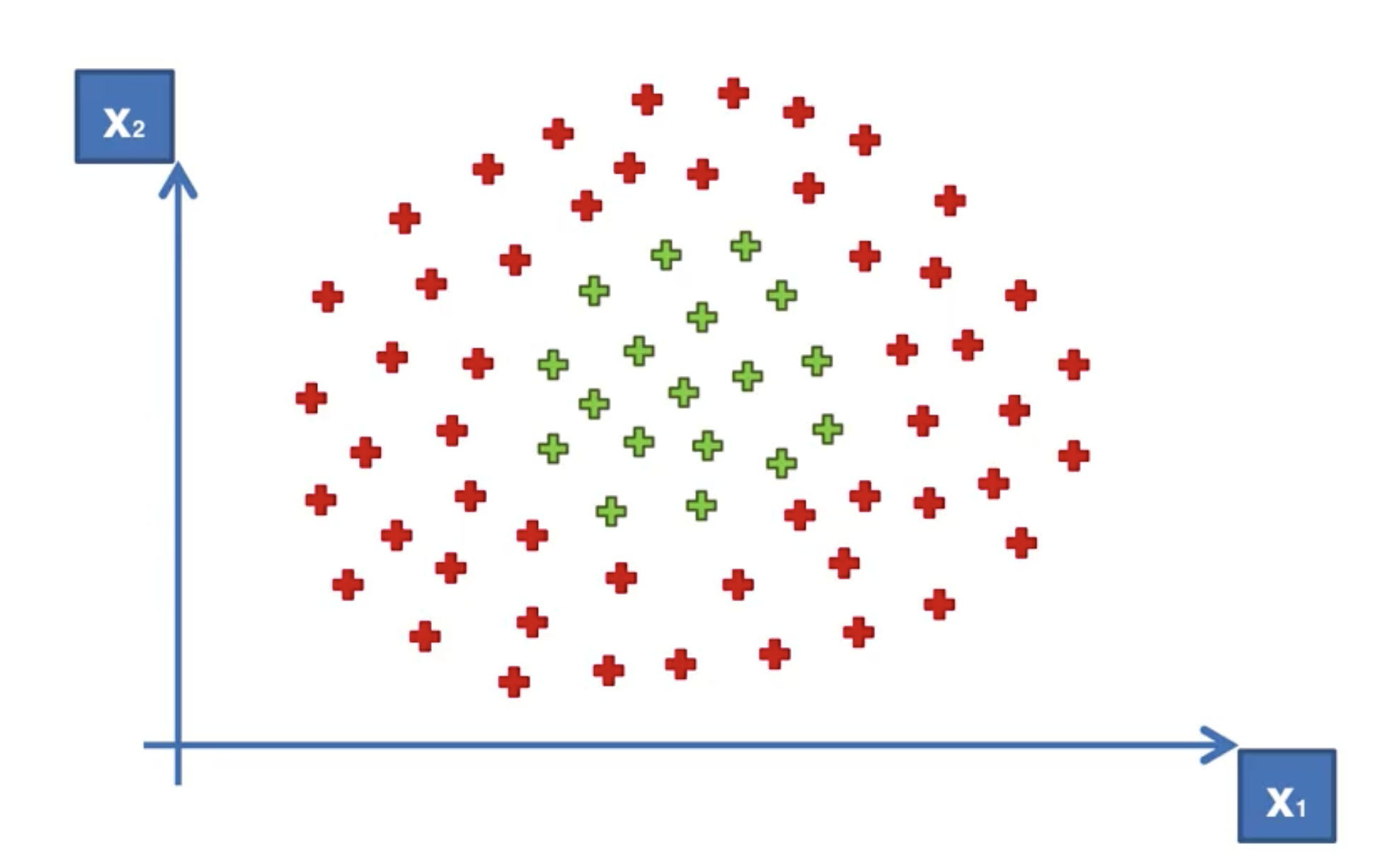
我們顯然無法找到一條直線來將這兩類資料分開。這時,我們可以使用核函數來將資料映射到高維空間,然後在高維空間中找到一個分割超平面。
我們稱其為“高維投射”。然而這個過程是非常耗時的。這時,我們可以使用核函數來簡化這個過程。
常用的核函數有:
- 高斯鏡像核函數(Gaussian RBF Kernel),公式為 。其中 是自變數, 是支援向量, 是一個參數。
- Sigmod 核函數,公式為 。其中 和 是參數。
- 多項式核函數,公式為 。其中 是一個參數, 是次數。當 時,即為線性核函數。
樸素貝葉斯
樸素貝葉斯,或稱單純貝氏分類器,是一種基於貝葉斯定理的分類算法。貝葉斯定理是一種概率定理,用於計算在給定條件下的概率。
貝葉斯定理
貝葉斯定理的公式為:。其中 是在給定 B 的條件下 A 的概率, 是在給定 A 的條件下 B 的概率, 和 是 A 和 B 的概率。這個公式對於有學過統計學的人來說應該不陌生。
我們舉一個直觀的示例來解釋這個公式。假設我們有一種零件,一家工廠的兩台機器都可以生產這種零件。現在知道如下資訊:
- 機器 1 的生產效率是 30/hr,機器 2 的生產效率是 20/hr。
- 所有的零件中,次品率是 1%。
- 所有的次品中,有 50% 是由機器 1 生產的。
現在問,由機器 2 生產的零件是次品的概率是多少?
在上面的問題中,我們可以使用貝葉斯定理來解決。首先,我們可以計算 和 :
接下來我們可以計算 :
而 ,且 。
所求的是 ,即在機器 2 生產的零件是次品的概率。根據貝葉斯定理,我們可以得到:
樸素貝葉斯分類器
我們有這樣一個例子:根據不同人群的年齡和薪水,來預測此人出行是步行還是開車。接下來,我們要判斷當有一個新的人加入時,他會是步行還是開車。
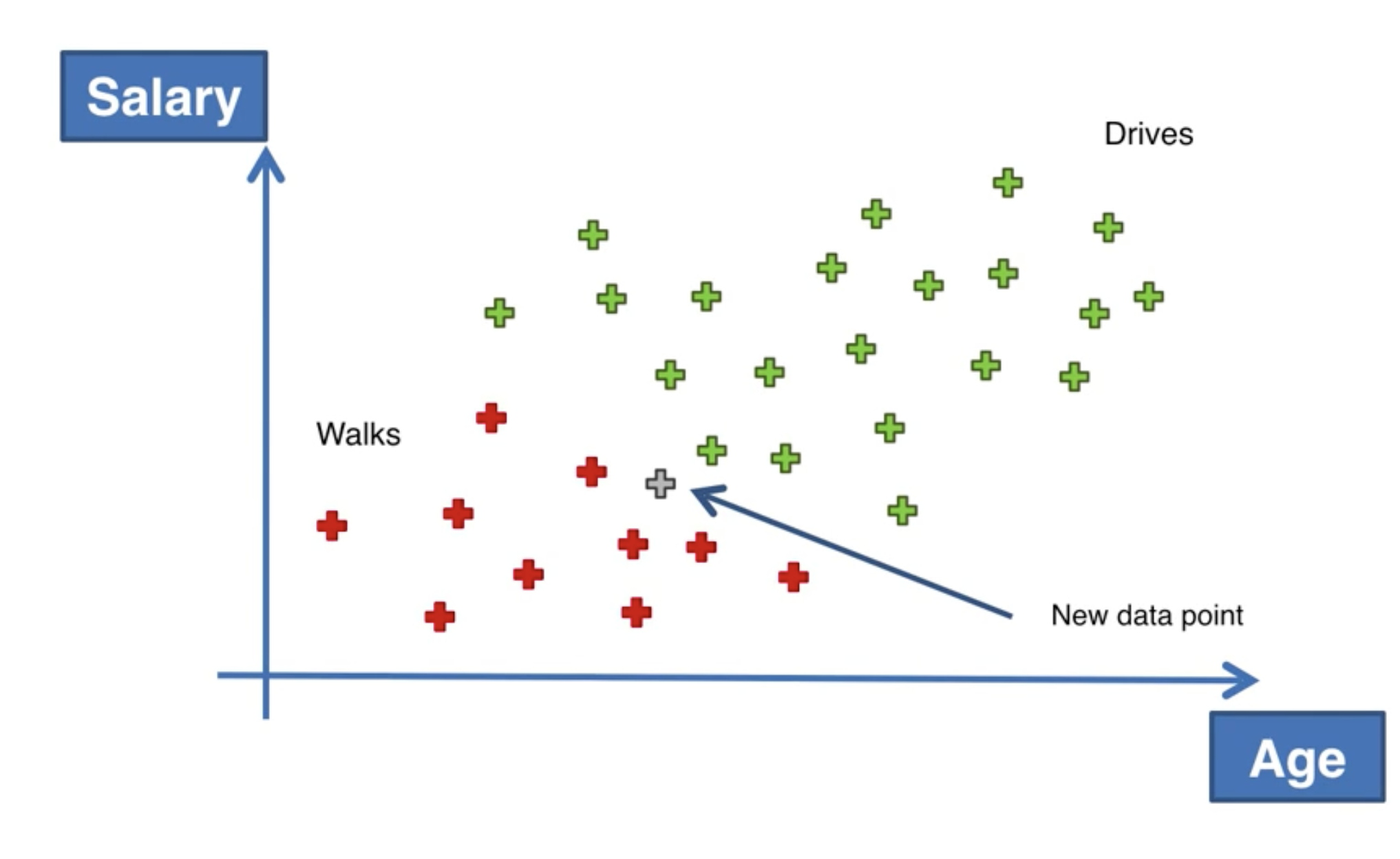
如果我們用樸素貝葉斯算法來計算,就轉變成了如下公式:
什麼是 X?X 是一個向量,包含了年齡和薪水,稱為特徵。 是在步行的情況下,特徵似然的概率。 是步行的概率。 是特徵似然的概率。
我們來逐步來看。
- 和 是我們的先驗概率。這是我們對步行和開車的概率的初始估計。,。
- 是我們的邊緣似然。這是我們的特徵似然的概率。。
- 和 是我們的似然。這是在步行和開車的情況下,特徵似然的概率。,。
而後我們即可求取我們的後驗概率。
在 Python 中實現樸素貝葉斯
from sklearn.naive_bayes import GaussianNB
# 創建分類器classifier = GaussianNB()
# 擬合classifier.fit(X_train, Y_train)
# 預測Y_pred = classifier.predict(X_test)決策樹
決策樹是一種監督學習算法,用於分類和回歸。決策樹透過將資料集分成更小的子集,來預測目標的值。決策樹的目標是創建一個樹狀結構,其中每個節點都是一個特徵,每個葉子節點都是一個類別。
還是舉例來說明。

畫線!
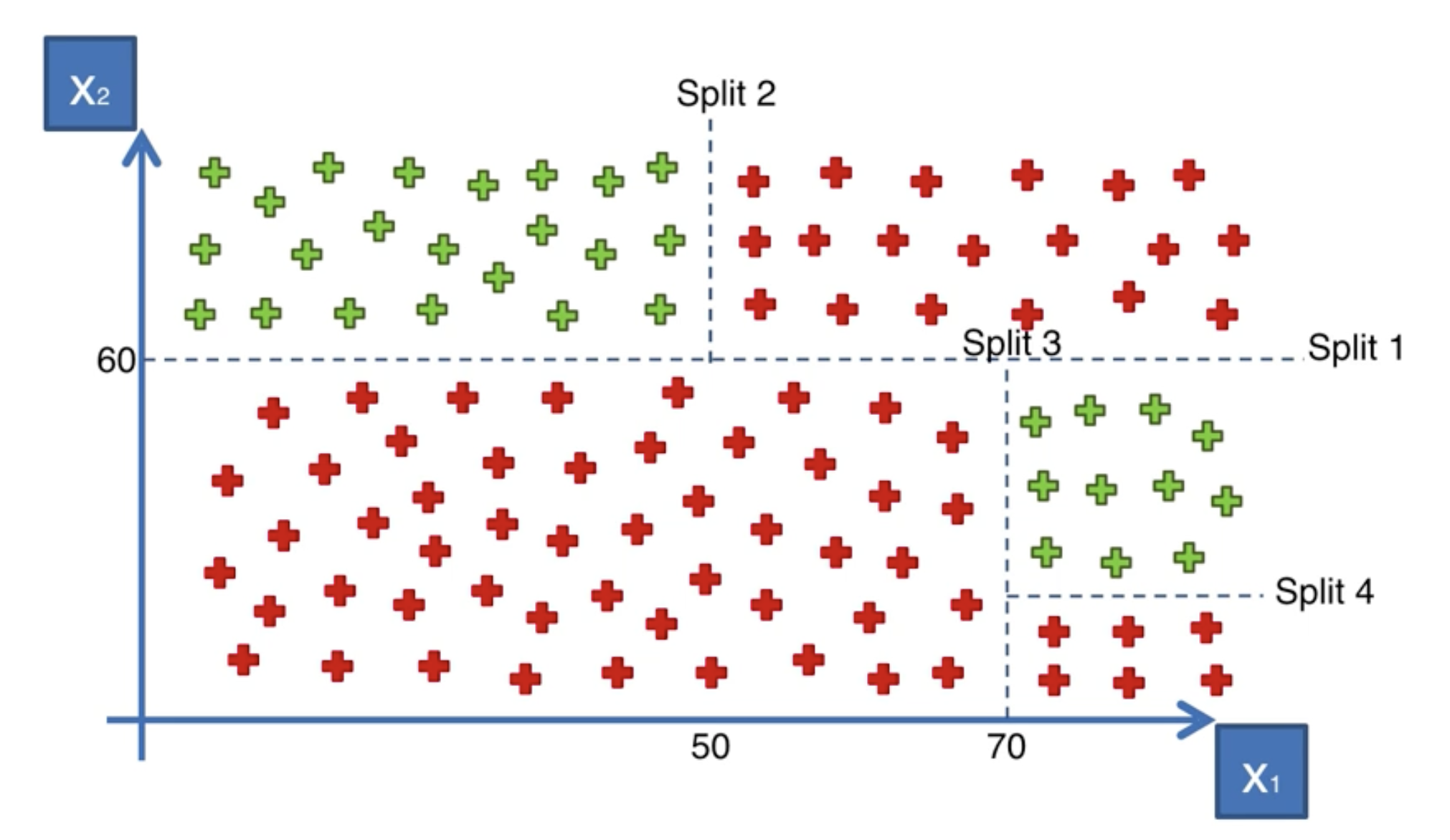
決策樹的問題,事實上就是找到最佳分隔線的問題。
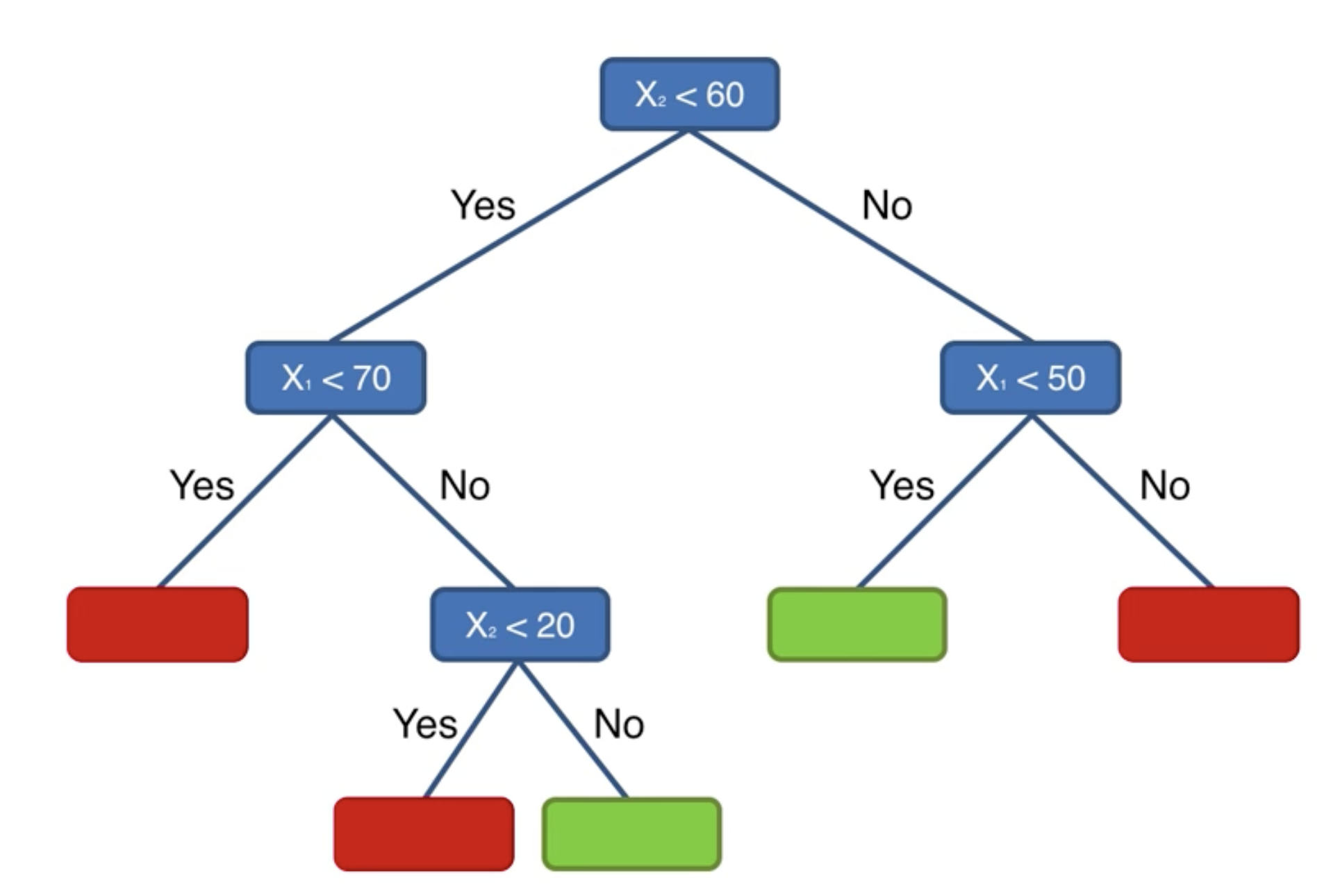
我們在 Python 中實現決策樹。
from sklearn.tree import DecisionTreeClassifier
# 創建分類器classifier = DecisionTreeClassifier(criterion='entropy', random_state=0) # 這裡的 criterion 是一個參數,可以是 'gini' 或 'entropy',分別表示使用基尼不純度或熵
# 擬合classifier.fit(X_train, Y_train)
# 預測Y_pred = classifier.predict(X_test)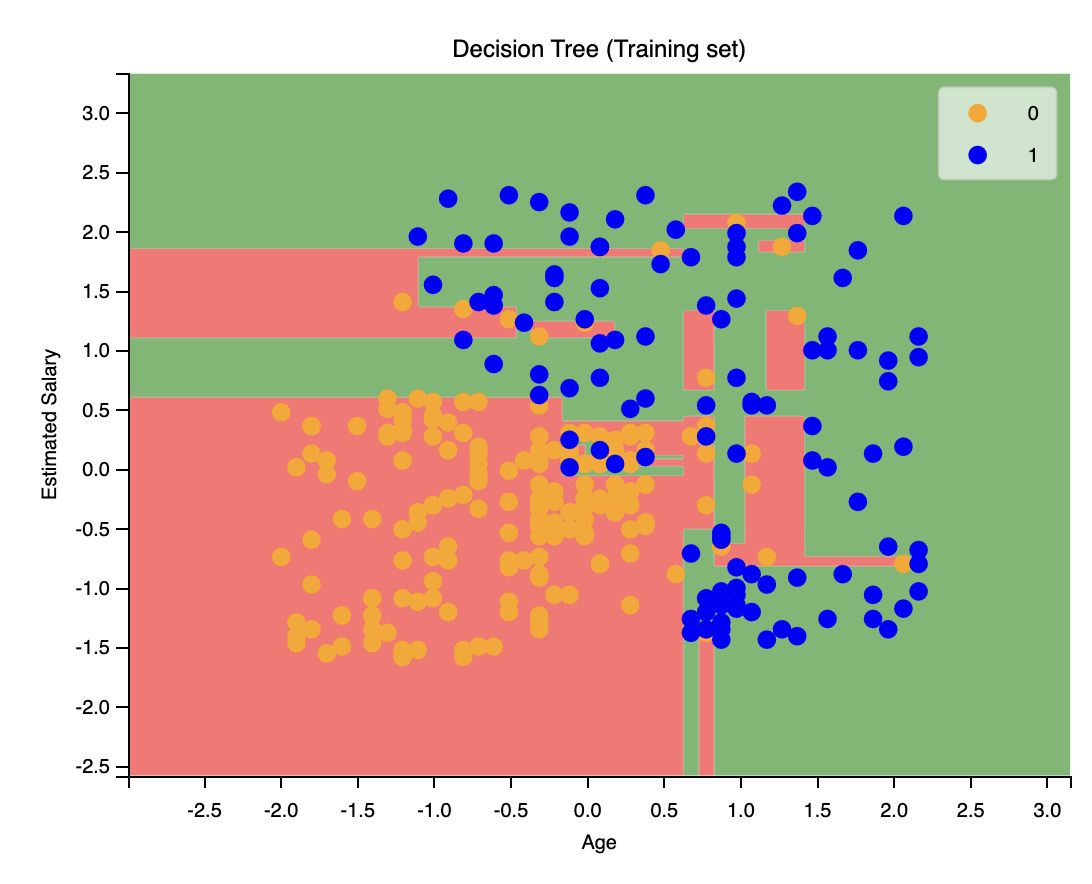
顯然,該圖像存在過擬合的問題。
隨機森林
隨機森林是一種集成學習算法,用於分類和回歸。隨機森林透過組合多個決策樹來提高預測準確性。隨機森林的目標是創建多個決策樹,然後將它們組合起來,以提高預測準確性。
什麼叫集成學習?集成學習是一種機器學習技術,透過組合多個模型來提高預測準確性。
它的步驟如下:
- 隨機選擇一個樣本子集。即選擇一個 random K data points from the Training set。
- 根據這個子集,建立一個決策樹。在建立決策樹的過程中,我們會隨機選擇特徵。
- 重複步驟 1 和 2,直到我們有 N 棵決策樹。
- 為了預測新的資料,我們將所有的決策樹的預測結果進行投票。
我們在 Python 中實現隨機森林。
from sklearn.ensemble import RandomForestClassifier
# 創建分類器classifier = RandomForestClassifier(n_estimators=10, criterion='entropy', random_state=0) # 這裡的 n_estimators 是一個參數,表示森林中樹的數量
# 擬合classifier.fit(X_train, Y_train)
# 預測Y_pred = classifier.predict(X_test)分類模型性能評價及選擇
假陽性和假陰性
- 假陽性(False Positive):實際上是負面的,但被分類為正面。即統計學上的第一類錯誤。
- 假陰性(False Negative):實際上是正面的,但被分類為負面。即統計學上的第二類錯誤。
混淆矩陣
混淆矩陣是一個表格,用於評估分類模型的性能。混淆矩陣的列(row)表示預測類別,欄(column)表示實際類別。
比如下面的一個混淆矩陣:
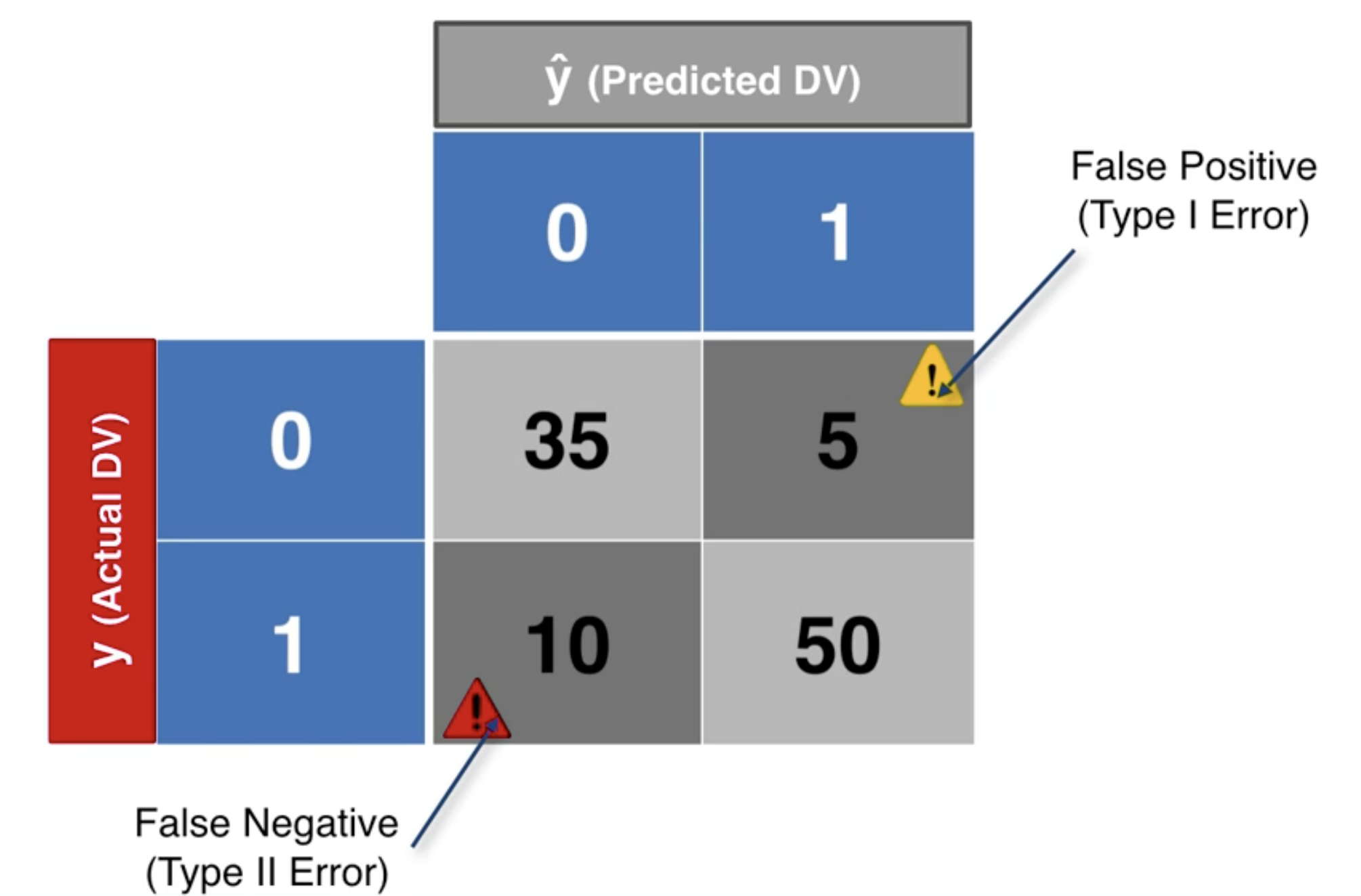
從上面的混淆矩陣可以算出:
- 準確率:
- 錯誤率:
然而,混淆矩陣有的時候並不能夠很好地評估模型的性能。因此,我們需要使用其他的指標。
比如,我們有如下混淆矩陣:
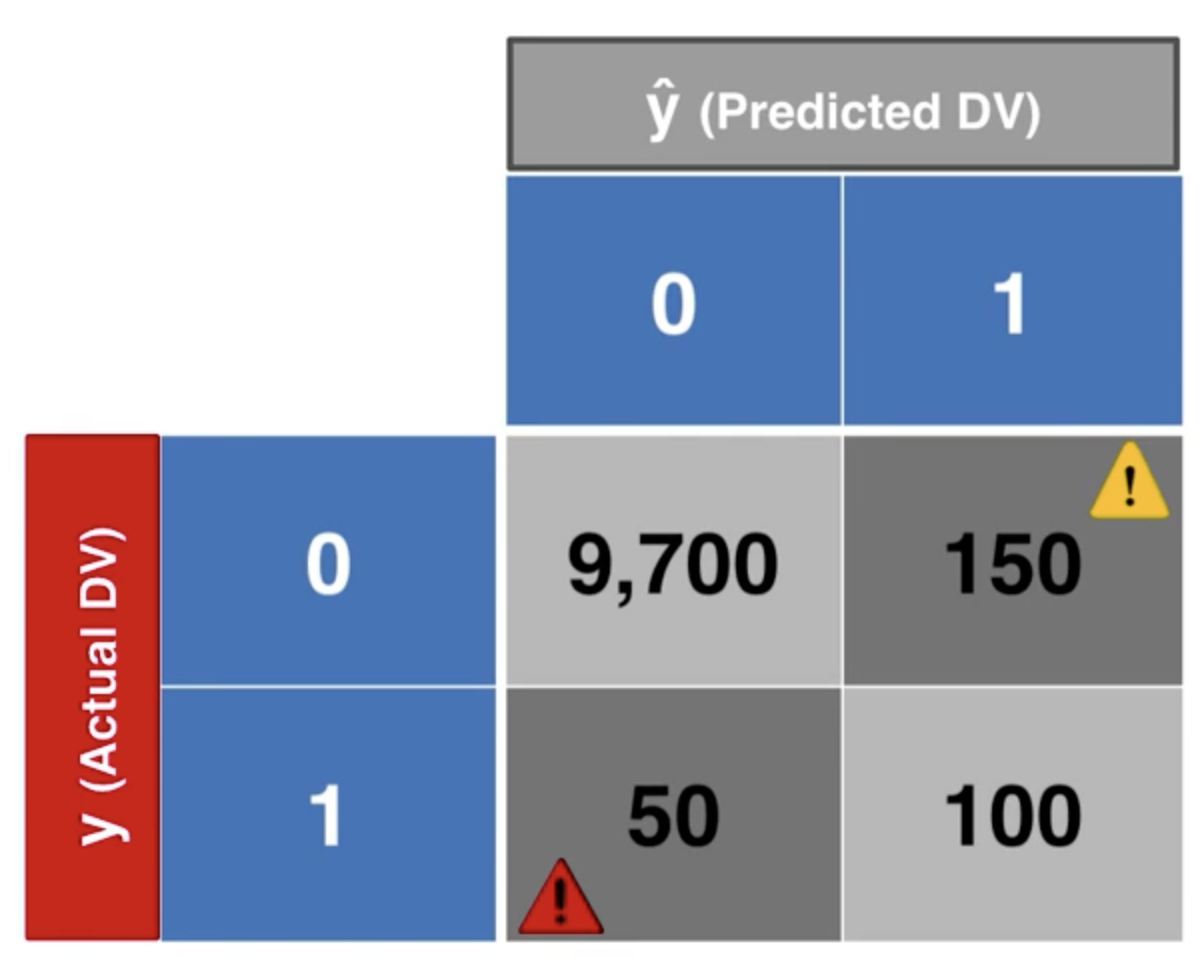
我們可以計算準確率:
但是,這個準確率並不能夠很好地反映模型的性能。假設我們像個傻瓜一樣,不管什麼情況都預測為陰性,我們會得到下面的混淆矩陣:
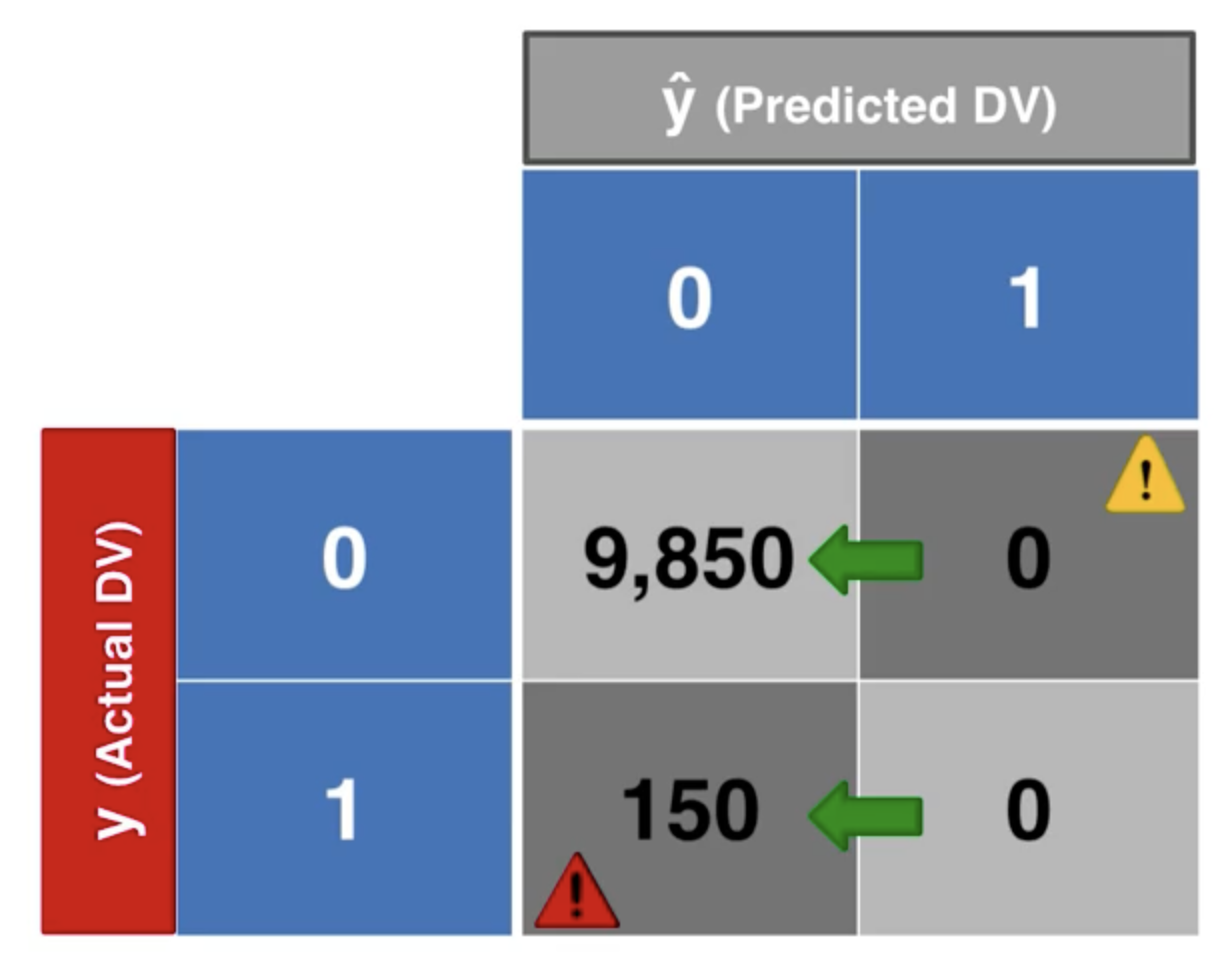
我們計算它的準確率為 98.5%。
這就非常有意思了,這個模型的準確率甚至比我們之前的模型還要高,儘管這是一個非常糟糕的模型。
於是,我們陷入了“準確率悖論”。這就說明,我們需要一些更好的指標來評估模型的性能。
累積準確曲線 CAP
累積準確曲線(CAP)是一種用於評估分類模型性能的圖表。CAP 曲線將實際正例的累積數量與預測正例的累積數量進行比較。
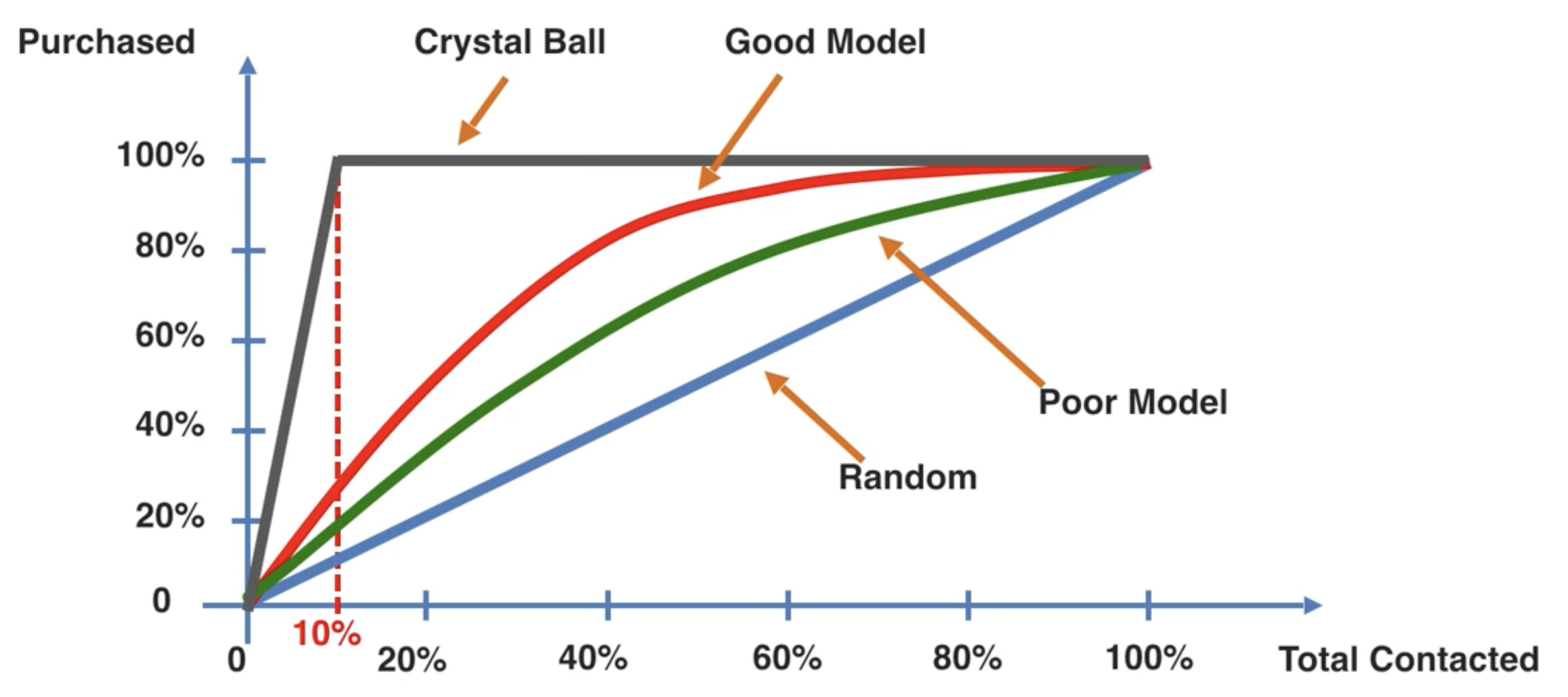
藍色的曲線,我們稱為 Random,即隨機猜測。紅色和綠色的曲線,我們稱為 Model,即應用我們的模型之後,得到的結果。而黑色的線,我們則稱為 Crystal Ball,即如果我們的模型是完美的,那麼我們的結果就是這條線。
我們定義 Crystal Ball Area(CBA)為 Crystal Ball 曲線下的面積,Model Area(MA)為 Model 曲線下的面積,Random Area(RA)為 Random 曲線下的面積。
則定義 AR(Accuracy Ratio)為 ,即 Model 曲線同 Random 與 Crystal Ball 曲線同 Random 曲線下的面積的比值。它的範圍是 0 到 1,越接近 1,表示模型越好。
經驗法則:取 x = 0.5,對應的模型 y 的值為 Y,如果:
- Y < 0.6,則模型為 Rubbish
- 0.6 < Y < 0.7,則模型為 Poor
- 0.7 < Y < 0.8,則模型為 Good
- 0.8 < Y < 0.9,則模型為 Very Good
- 0.9 < Y,則模型為 Too Good
K-均值聚類
K-均值聚類可以用來做什麼?K-均值聚類是一種無監督學習算法,用於將資料集分為 K 個簇。K-均值聚類的目標是找到 K 個簇,使得每個樣本都屬於其中一個簇。
K-均值聚類的步驟如下:
- 首先選擇想要區分的類別個數 K。
- 隨機選擇 K 個點作為中心,中心不必是一個樣本。
- 將每個樣本分配到最近的中心。
- 更新中心。
- 重複步驟 3 和 4,直到中心不再改變。
我們不難看出,在這個過程中,最重要的是中心點的選擇。不同的初始中心點選擇,會導致不同的結果。這被稱為“初始化陷阱”。解決方案,使用 K-Means++。但是我們不必深究,因為 scikit-learn 已經幫我們解決了這個問題。K-Means++ 是 scikit-learn 的預設初始化方法。
關於中心點的選擇,我們需要確定中心點的個數,即 K。有沒有一種科學的方法來確定 K 呢?有的,稱為 Elbow Method。Elbow Method 是一種用於確定 K 的方法,透過繪製 K 和 WCSS(Within-Cluster Sum of Squares)之間的關係圖,找到一個“拐點”。
WCSS(組內平方和)的公式如下:
通俗來講,WCSS 是每個樣本到它所屬簇的中心的距離的平方和的和。
我們不難看出,WCSS 是一個隨著 K 的增加而減小的函數。因此,我們可以透過繪製 K 和 WCSS 之間的關係圖,找到一個“拐點”,即 Elbow Point,來確定 K。
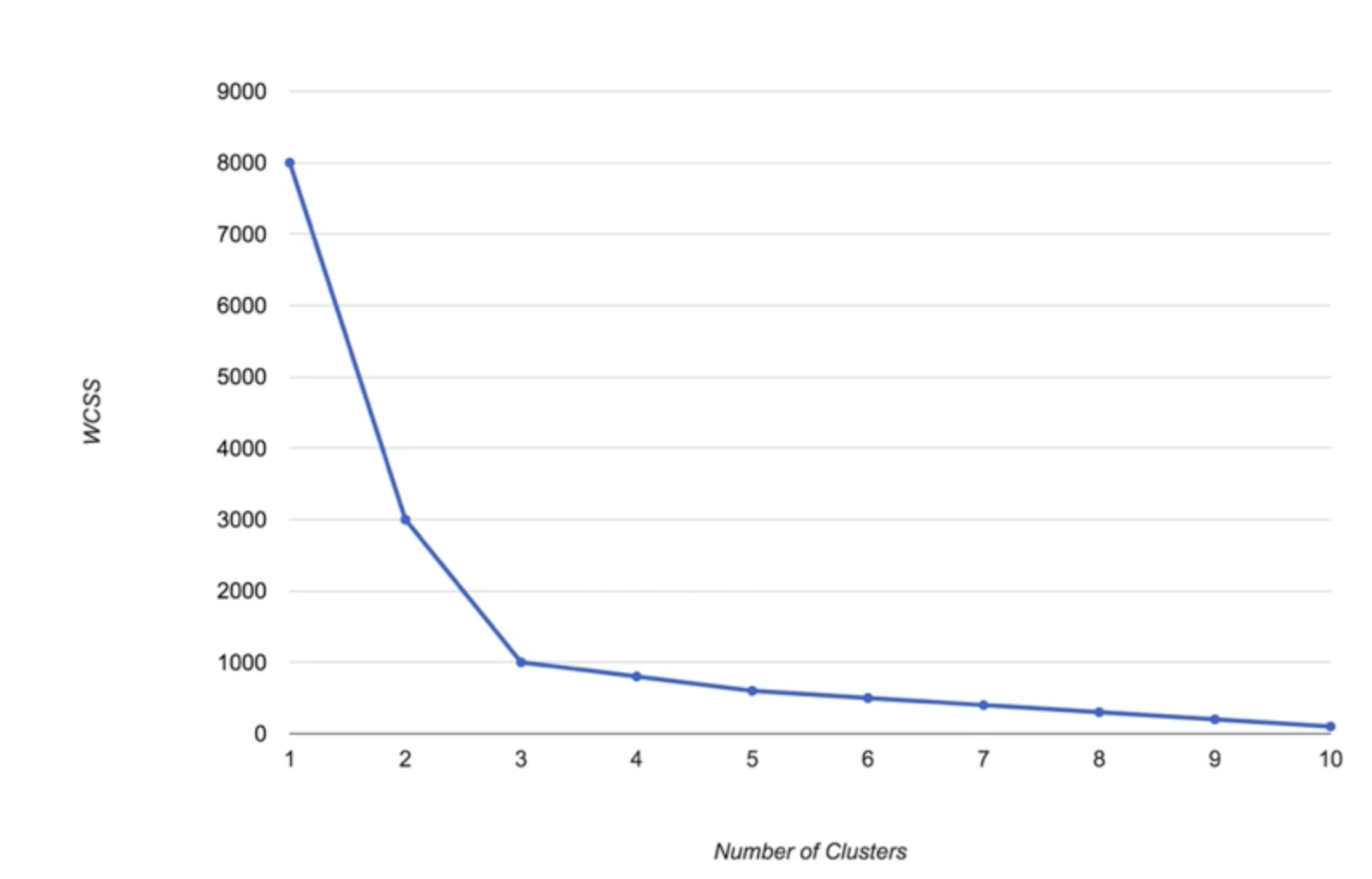
接下來,我們在 Python 中實現 K-均值聚類。
# 選擇 Kfrom sklearn.cluster import KMeans
# 初始化 wcss 向量wcss = []
for i in range(1, 11): # 這裡的 11 表示我們選擇的 K 的範圍從 1 到 10 kmeans = KMeans(n_clusters=i, init='k-means++', random_state=0) # 這裡的 init 是一個參數,表示初始化方法 kmeans.fit(X) # 用選定的 K 擬合 X wcss.append(kmeans.inertia_) # 將 WCSS 結果加入 wcss 向量
# 繪製 K 和 WCSS 之間的關係圖,找出 Elbow Pointplt.plot(range(1, 11), wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()假設我們找到的 Elbow Point 是 5,那麼我們可以選擇 K = 5,對資料進行 K-均值聚類分析。
kmeans = KMeans(n_clusters=5, init='k-means++', random_state=0)
Y_kmeans = kmeans.fit_predict(X)我們可以使用視覺化來看一下結果。
plt.scatter(X[Y_kmeans == 0, 0], X[Y_kmeans == 0, 1], s = 100, c = 'red', label = 'Cluster 1')
plt.scatter(X[Y_kmeans == 1, 0], X[Y_kmeans == 1, 1], s = 100, c = 'blue', label = 'Cluster 2')
plt.scatter(X[Y_kmeans == 2, 0], X[Y_kmeans == 2, 1], s = 100, c = 'green', label = 'Cluster 3')
plt.scatter(X[Y_kmeans == 3, 0], X[Y_kmeans == 3, 1], s = 100, c = 'cyan', label = 'Cluster 4')
plt.scatter(X[Y_kmeans == 4, 0], X[Y_kmeans == 4, 1], s = 100, c = 'magenta', label = 'Cluster 5')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 300, c = 'yellow', label = 'Centroids')
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()得到如下結果:
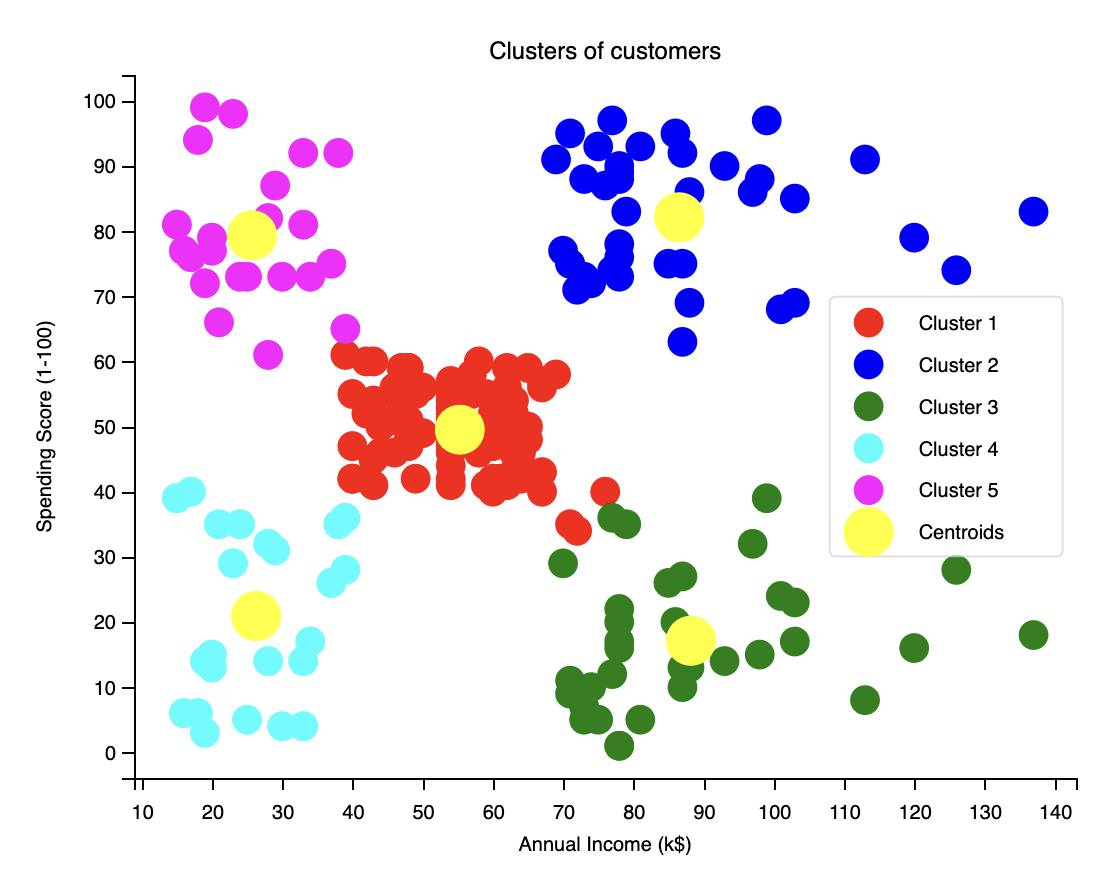
關聯規則學習:先驗演算法
關聯規則學習是一種用於發現資料集中項目之間關係的技術。先驗演算法是一種用於發現關聯規則的技術。先驗演算法透過計算項目之間的支持度和置信度來發現關聯規則。
世界零售巨頭沃爾瑪公司曾經發現,在某一個時段,當顧客購買尿布時,他們中的大多數也會購買啤酒。這是一個非常有趣的發現。後來證實,這是因為在這個時段過來購買尿布的顧客大多是年輕的寶爸,他們會在購買完尿布之後,順便再買一些啤酒。先驗算法就是用來發現這種關聯規則的。
先驗演算法中,有三個重要的概念:支援度、置信度和提升度。
- 支援度(Support):指的是包含項目集 X 的交易的百分比。即 。比如,在 100 個人中,有多少個人看過《放牛班的春天》這部電影。
- 置信度(Confidence):指的是包含項目集 X 和 Y 的交易的百分比。即 。比如,在 100 個人中,有 40 人看過《泰坦尼克號》,在這 40 個人中,有多少人看過《放牛班的春天》。
- 提升度(Lift):指的是包含項目集 X 和 Y 的交易的百分比,相對於包含 Y 的交易的百分比的提升。即 。比如,看過《泰坦尼克號》的人中,看過《放牛班的春天》的人的比例,相對於看過《放牛班的春天》的人的比例。
先驗演算法的步驟如下:
- 設定最小支援度和最小置信度。
- 把所有比最小支援度大的項目集作為候選集。
- 把候選集中所有比最小置信度大的規則作為關聯規則。
- 使用降序提升度來排序這些規則。
我們在 Python 中實現先驗演算法。
from apyori import apriori
# 設定最小支援度和最小置信度rules = apriori(transactions, min_support = 0.003, min_confidence = 0.2, min_lift = 3, min_length = 2) # 這裡的 transactions 是我們的資料集
# 結果results = list(rules)強化學習
強化學習是一種機器學習技術,用於訓練智能體,使其在環墋中學習。強化學習的目標是使智能體學會在環墋中採取最佳的行動,以最大化獎勵。
我們先來看一個具體的例子——多臂賭博機的問題。多臂賭博機是一種賭博機,由多個單臂賭博機組成。每個單臂賭博機都有一個固定的機率分佈。我們的目標是找到一種策略,使得在有限的時間內,獲得最大的獎勵。

假如我們知道這些賭博機的機率分佈,我們可以只玩機率最大的那個賭博機。但是,如果我們不知道這些機率分佈,我們該怎麼辦呢?這就需要我們一次一次嘗試來找到最佳策略。
這個過程我們叫做 “探索-利用” 問題。探索是指我們嘗試不同的策略,利用是指我們利用我們已經知道的信息。我們需要找到一個平衡點,使得在探索和利用之間取得最佳的平衡。而 “遺憾” 則是指我們在探索的過程中,錯過了一些機會。探索的次數越多,遺憾就越大;但是,探索的次數越少,我們找到最佳策略的機會就越小。
上置信界算法 UCB
上置信界算法(Upper Confidence Bound,UCB)是一種可以用於解決多臂賭博機問題的算法,也是一種經典的強化學習算法。UCB 算法透過計算每個賭博機的上置信界,來決定下一步採取的行動。
我們重新來補充一個完整的多臂賭博機的問題。
現在,某公司在某個網站有多種不同的廣告。每次當用戶造訪這個網站的時候,我們稱這是一“輪”,在每一輪中,我們都要向用戶展示這些廣告中的一個。在第 輪裡,廣告 給予的獎勵是 ,。假如用戶 click 了廣告 ,則 ;否則 。我們的目標是找到一個策略,使得在有限的時間內,獲得最大的獎勵。
UCB 算法的步驟如下:
- 對於每個 ,計算兩個數值: 和 。其中 是廣告 被選中的次數, 是廣告 的獎勵總和。
- 根據以上兩個數值,我們計算以下數值:
- 平均獎勵:
- 在第 n 輪的置信區間 ,其中
- 我們選擇擁有最大 UCB 的廣告 i,其中 UCB 定義為 。
我們在 Python 中實現 UCB 算法。
import math
# 第一步,計算 N_i(n) 和 R_i(n)N = 10000 # 輪數d = 10 # 廣告數numbers_of_selections = [0] * d # 每個廣告被選中的次數sums_of_rewards = [0] * d # 每個廣告的獎勵總和ads_selected = [] # 選擇的廣告total_reward = 0 # 總獎勵
# 第二步for n in range(0, N): ad = 0 # 最大 UCB 的廣告 max_upper_bound = 0 # 最大 UCB for i in range(0, d): if numbers_of_selections[i] > 0: average_award = sums_of_rewards[i] / numbers_of_selections[i] # 平均獎勵 delta_i = math.sqrt(3/2 * math.log(n + 1) / numbers_of_selections[i]) # Delta_i(n) upper_bound = average_award + delta_i # UCB else: upper_bound = 1e400 if upper_bound > max_upper_bound: max_upper_bound = upper_bound ad = i # 選擇擁有最大 UCB 的廣告 i ads_selected.append(ad) reward = dataset.values[n, ad] # 獎勵 numbers_of_selections[ad] = numbers_of_selections[ad] + 1 sums_of_rewards[ad] = sums_of_rewards[ad] + reward total_reward = total_reward + reward我們可以使用視覺化來看一下結果。
plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()這一部分終於涉及到手寫算法的部分了。算法這種東西,就是看著能勉強理解,一上手就廢廢的,這也正常。所以如果讀者這一段讀不懂,可以多讀幾遍試一下。
Thompson Sampling
Thomas Sampling 是另一種可以用於解決多臂賭博機問題的算法,也是一種經典的強化學習算法。Thomas Sampling 算法透過計算每個賭博機的機率分佈,來決定下一步採取的行動。
Thomas Sampling 算法的步驟如下:
- 在每一輪 n 中,對於每個廣告 i,我們計算以下內容:
- 在第 輪之前,廣告 得到獎勵 1 的次數
- 在第 輪之前,廣告 得到獎勵 0 的次數
- 對於每一個廣告 ,我們利用以下 beta 概率分配抽取一個隨機數 :
- 我們選擇擁有最大 的廣告 j。
我們尚看到,Thomas Sampling 算法的核心是 beta 概率分配。這裡我們介紹貝葉斯推斷。
上面的例子中,當廣告 被選擇後,我們將得到的獎勵記為 ,(即用戶有 click 廣告)的概率為 ,等於 的概率為 。 遵循伯努利分配:。
這些概率 是未知的。但在遊戲過程中,每一個 都遵守擁有參數 的 beta 分配。那麼對於每一個廣告 , 的概率密度函數是:
假設我們選取了某個廣告 ,得到了新的觀察資料 。那麼我們可以更新 的概率分佈:
在第 輪,我們可以透過抽取 來選擇廣告 。
好,到現在為止,如果你已經被這一堆數學公式搞得頭昏腦脹,那也是正常的。這些數學公式的背後,是一個很複雜的數學理論。但是,我們不需要深入理解這些數學理論,我們只需要靜靜地做一個 Method Caller 就好。
我們在 Python 中實現 Thomas Sampling 算法。
import random
# 第一步N = 10000 # 輪數d = 10 # 廣告數numbers_of_rewards_1 = [0] * dnumbers_of_rewards_0 = [0] * dads_selected = [] # 選擇的廣告total_reward = 0 # 總獎勵
# 第二步for n in range(0, N): ad = 0 # 最大 UCB 的廣告 max_random = 0 # 最大 UCB for i in range(0, d): random_beta = random.betavariate(numbers_of_rewards_1[i] + 1, numbers_of_rewards_0[i] + 1) if random_beta > max_random: max_random = random_beta ad = i ads_selected.append(ad) reward = dataset.values[n, ad] # 獎勵 if reward == 1: numbers_of_rewards_1[ad] += 1 else: numbers_of_rewards_0[ad] += 1 total_reward = total_reward + reward
# 視覺化plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()我們發現,不同於 UCB,Thomas Sampling 算法的結果是隨機的。這是因為 Thomas Sampling 算法是一種隨機算法,它透過抽取隨機數來決定下一步採取的行動。
自然語言處理
自然語言處理(Natural Language Processing,NLP)是一種人工智慧技術,用於處理和分析自然語言數據。NLP 可以用於文本分類、情感分析、機器翻譯等應用。
我們本期示例是:有一個餐廳,它的顧客在網站上留下了評論。我們的目標是透過這些評論來預測顧客對這家餐廳的評分。
文本清理
在進行自然語言處理之前,我們需要對文本進行清理。在此之前,我們先來介紹一下我們將要建立一個什麼樣的模型。
我們應用到的模型稱為“Bag of words”,中文名為“詞袋模型”。詞袋模型是一種用於文本分類的模型。在詞袋模型中,我們將文本轉換為一個向量,其中每個元素表示一個單詞的出現次數。
通俗講,我們建立了一個足夠大的“稀疏矩陣”,在這個矩陣中,每一行即為原來的一條記錄,而每一列則代表一個單詞。如果這個單詞在這條記錄中出現過,則對應的值為 1;否則為 0。
但是這樣會產生問題。英文是一種比較嚴謹的語言,時態、人稱、數量等等都是有規則的。比如 “love” 和 “loved”,甚至是 “Love”,在語義上都是一樣的,但是在詞袋模型中,它們被視為完全不同的單詞。這樣就會導致模型的不準確。因此,在建立詞袋模型之前,我們需要對文本進行清理,以生成足以應用到模型上的高質量資料。
文本清理第一步,將所有的數字、標點符號等等去掉,只保留字母。
import re
review = re.sub('[^a-zA-Z]', ' ', dataset['Review'][0])文本清理第二步,將所有的字母轉換為小寫。
review = review.lower()文本清理第三步,清理虛詞。虛詞對於我們的模型大多數時候是沒有意義的,因此我們需要將它們去掉。
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
review = review.split()
review = [word for word in review if not word in set(stopwords.words('english'))]文本清理第四步,詞根化。
from nltk.stem.porter import PorterStemmer然後把第三步的程式碼修改為:
ps = PorterStemmer()
review = [ps.stem(word) for word in review if not word in set(stopwords.words('english'))]文本清理第五步,將清理好的文本重新組合。
review = ' '.join(review)我們上面的程式碼是針對第一條評論進行的。如果我們要對所有的評論進行清理,我們可以將上面的程式碼放入一個迴圈中。
corpus = []
for i in range(0, 1000): review = re.sub('[^a-zA-Z]', ' ', dataset['Review'][i]) review = review.lower() review = review.split() ps = PorterStemmer() review = [ps.stem(word) for word in review if not word in set(stopwords.words('english'))] review = ' '.join(review) corpus.append(review)創建詞袋模型
接下來,我們將使用 scikit-learn 庫來創建詞袋模型。
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer(max_features = 1500)
X = cv.fit_transform(corpus).toarray()
Y = dataset.iloc[:, 1].values最大過濾
有一些單詞出現的次數非常少,比如人名等,這些單詞對於我們的模型來說是沒有意義的。我們可以使用最大過濾來去掉這些單詞。
cv = CountVectorizer(max_features = 1500)分類模型
我們使用 Naive Bayes 分類器來訓練我們的模型。
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.20, random_state = 0)
from sklearn.naive_bayes import GaussianNB
classifier = GaussianNB()
classifier.fit(X_train, Y_train)
Y_pred = classifier.predict(X_test)深度學習初見
深度學習、神經網路等概念,是近年來人工智慧領域的熱門話題。深度學習是一種機器學習技術,用於訓練神經網路。神經網路是一種模仿人類大腦的計算模型。
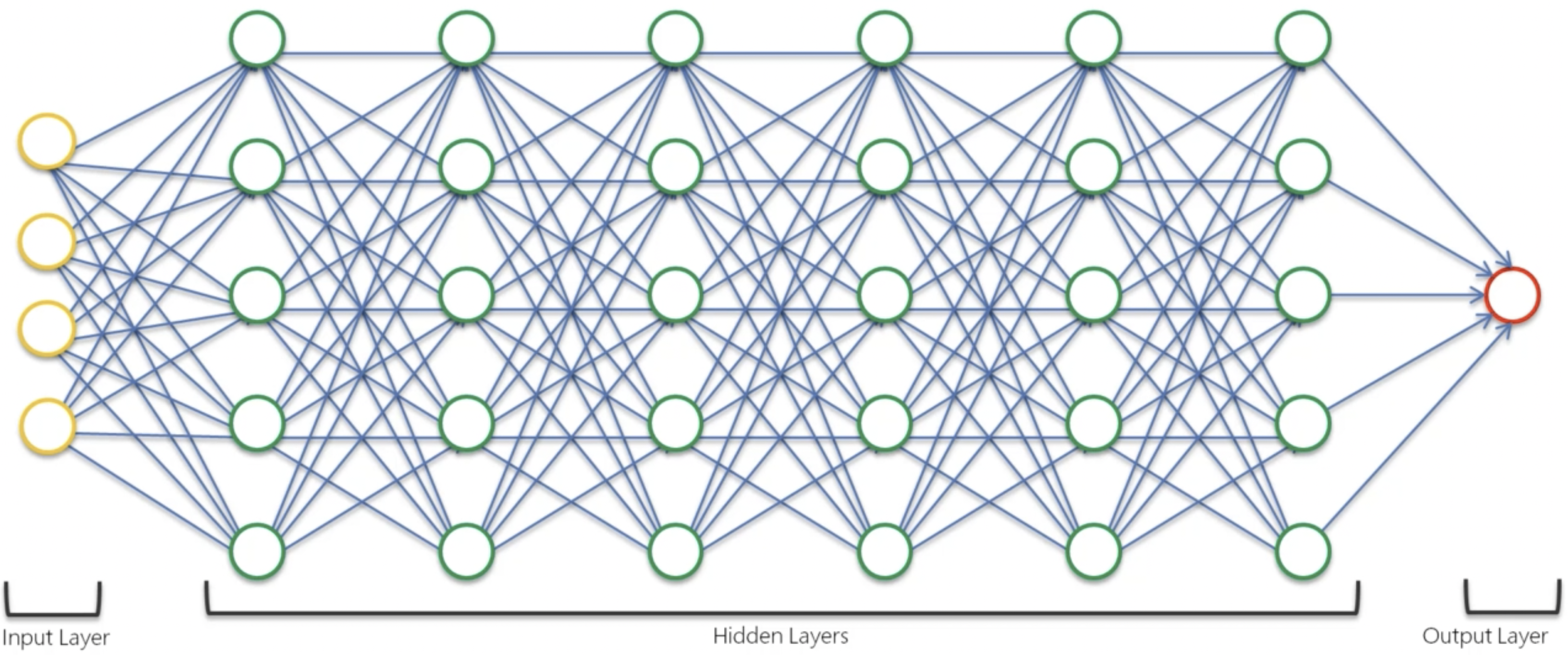
接下來的過程中,我們將只是進行一些關於深度學習的算法理論學習,不會涉及到 Python 程式碼。因為《機器學習 A-Z》這門課程發布的時間較早,所使用的框架尚為 Tensorflow 1.0,比較古老。當然,這些理論也是不完整的,但無所謂。在本文之後,筆者會繼續學習深度學習的相關知識,並在之後的文章中進行更深入的探討。
類神經網路 ANN
研究類神經網路,我們首先需要了解神經元的概念。由於筆者的專業是臨床醫學,因此對生物水平的神經元概念比較清晰,因此不在此贅述,如果你對神經元的概念不清楚,可以查閱相關資料。
我們直接來講機器學習水平的神經元概念。在機器學習水平的神經元中,每個神經元都有一個輸入和一個輸出。輸入是一個向量 ,輸出是一個激勵函數 。神經元的輸出是 ,其中 是權重, 是偏差。當我們訓練一個神經網路時,我們會調整權重和偏差,使得神經網路的輸出盡可能接近真實值。因此,權重和偏差是神經網路的核心。
激勵函數
激勵函數是神經元的輸出函數。激勵函數的作用是將神經元的輸入轉換為輸出。常用的激勵函數有 Sigmoid、ReLU、Tanh 等。
Threshold Function
閾值函數是一種二元激勵函數,當輸入大於閾值時,輸出為 1;否則為 0。
其公式為:
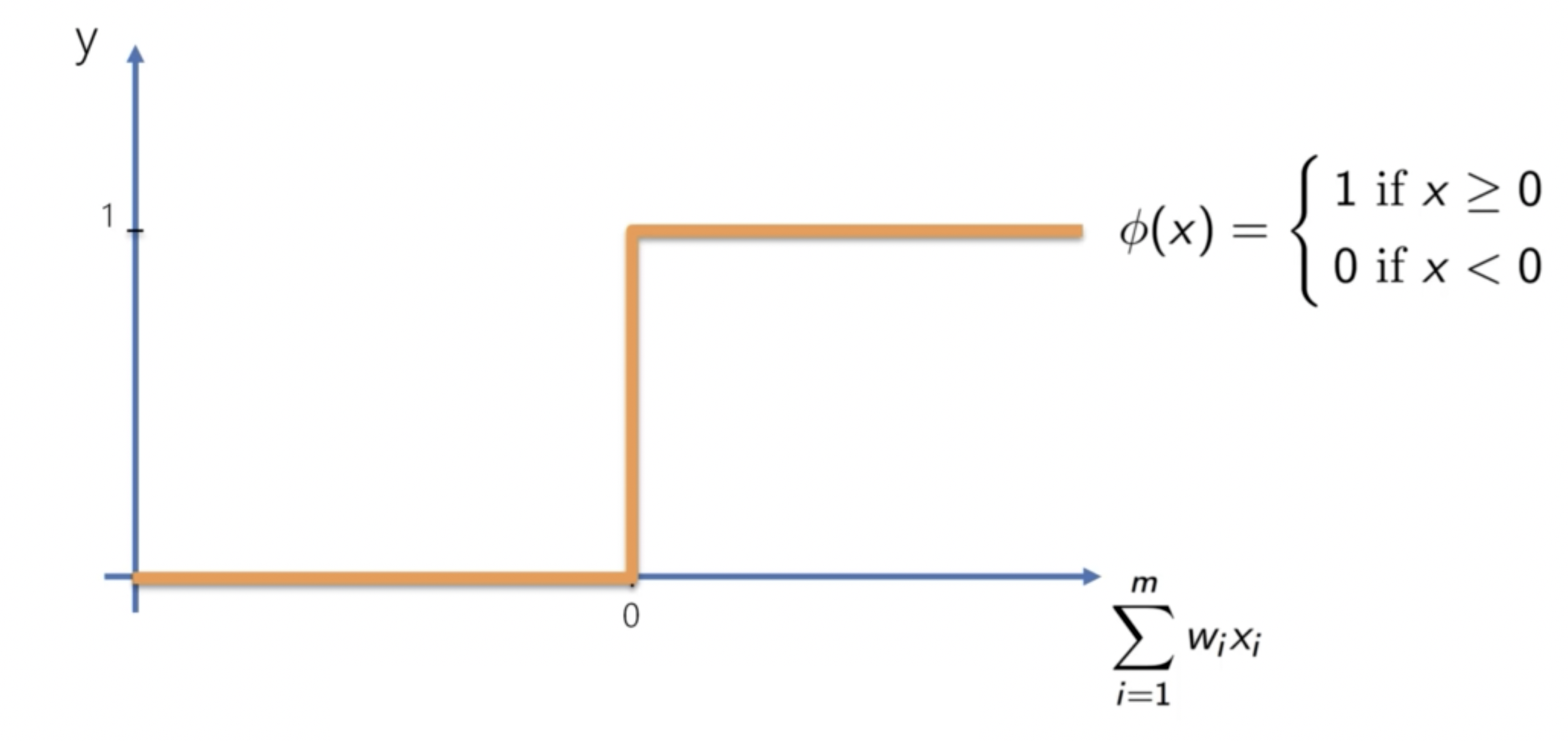
但是這個函數在實際應用中並不常見,因為它不可微。
Sigmoid Function
Sigmoid 函數通常被用於輸出層的激勵函數。其公式是:
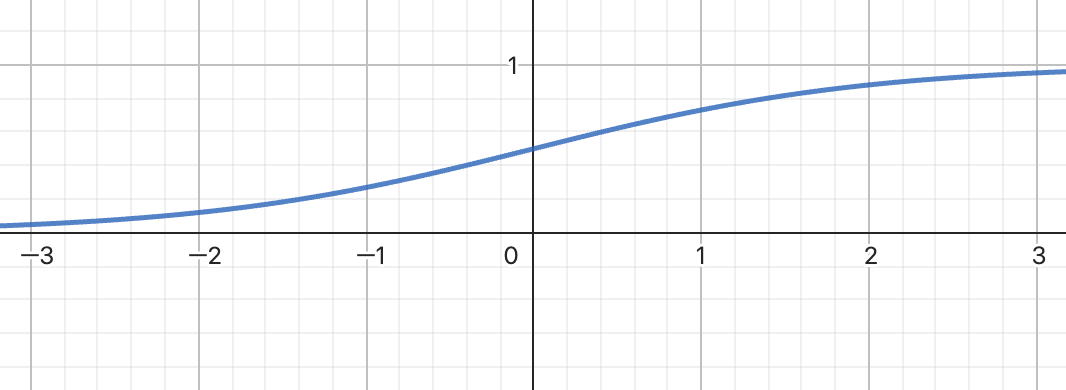
然而,其固有缺陷是當 非常大或非常小時,梯度會變得非常小,這將導致梯度消失問題。
ReLU Function
ReLU 函數是一種常用的激勵函數。其公式是:
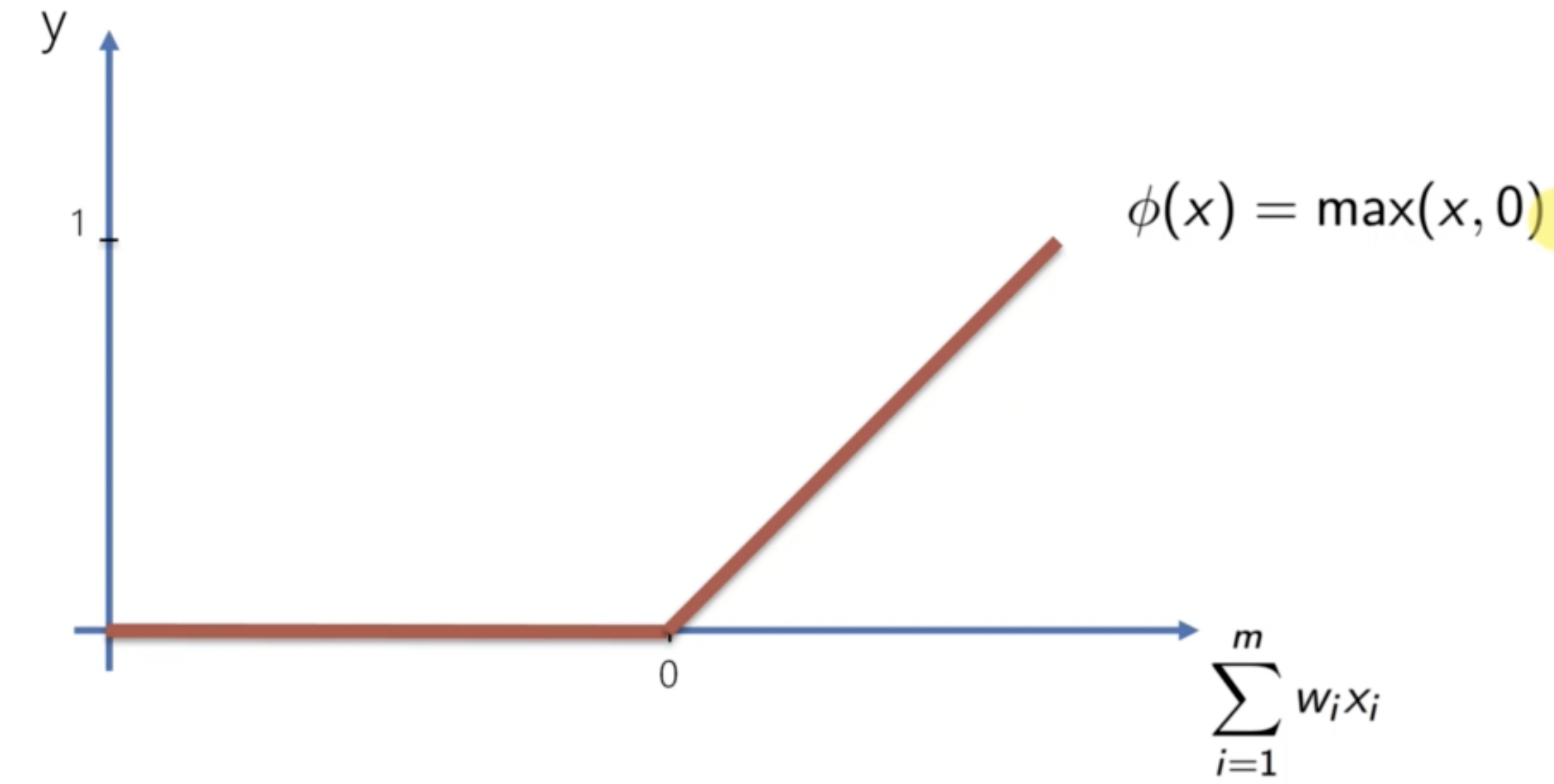
ReLU 函數的優點是計算速度快,並且不會有梯度消失問題。
Tanh Function
Tanh 函數是一種常用的激勵函數。其公式是:
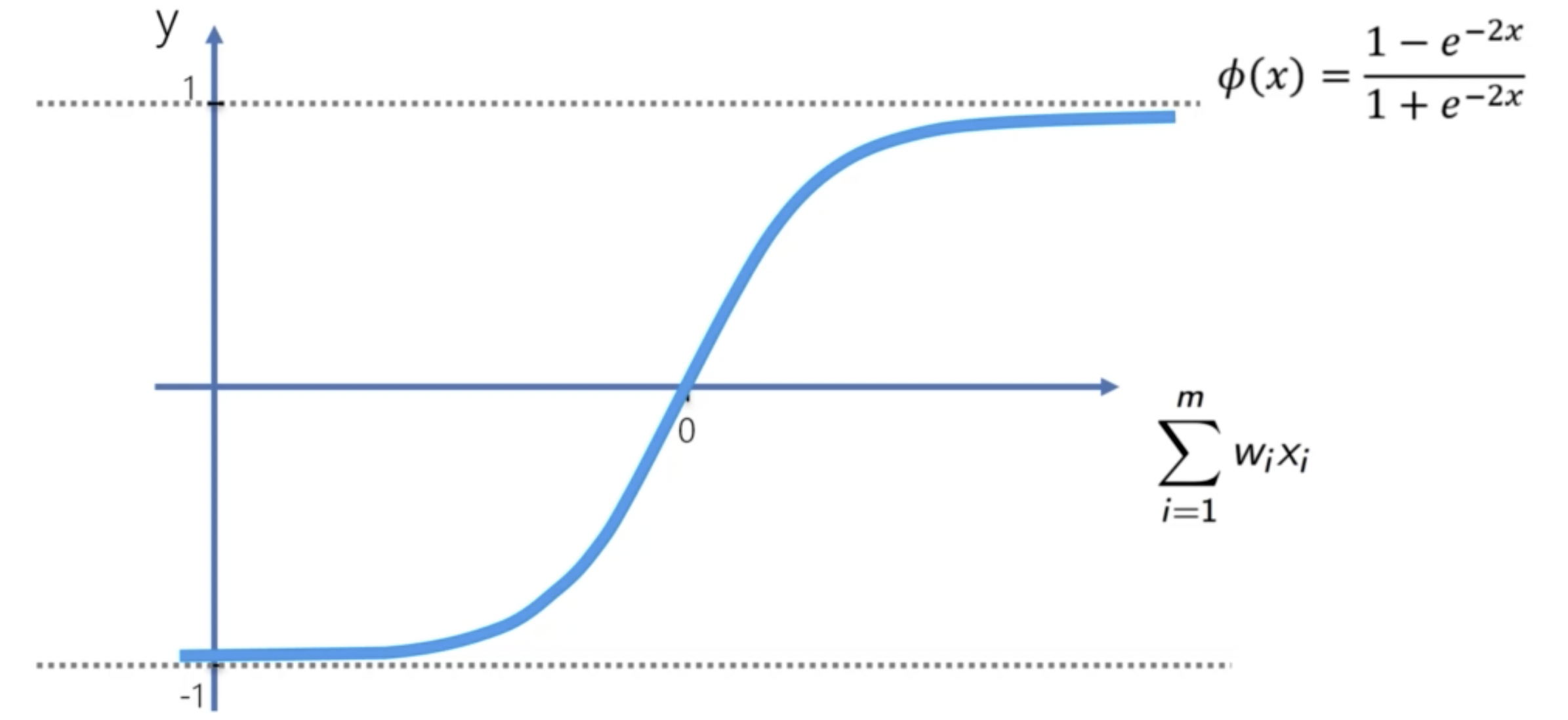
Tanh 函數的優點是可以將輸入歸一化到 -1 到 1 之間。
如何選擇激勵函數呢?這要看我們的輸出變數是什麼。如果是二元分類,我們可以使用 Threshold 函數或者 Sigmoid 函數。常見的搭配是:在隱藏層中使用 ReLU 函數,在輸出層中使用 Sigmoid 函數。
神經網路的運作方式
神經網路是由多個神經元組成的。神經網路的運作方式是:將輸入 通過多個神經元,經過激勵函數後,得到輸出 。
我們舉例說明。假設我們有一個已拟合的神經網路,我們希望使用這個神經網路來做房價預測。
我們的輸入是四個參數:房屋面積、房間個數、距市中心距離、房屋年齡。我們的輸出是房價。
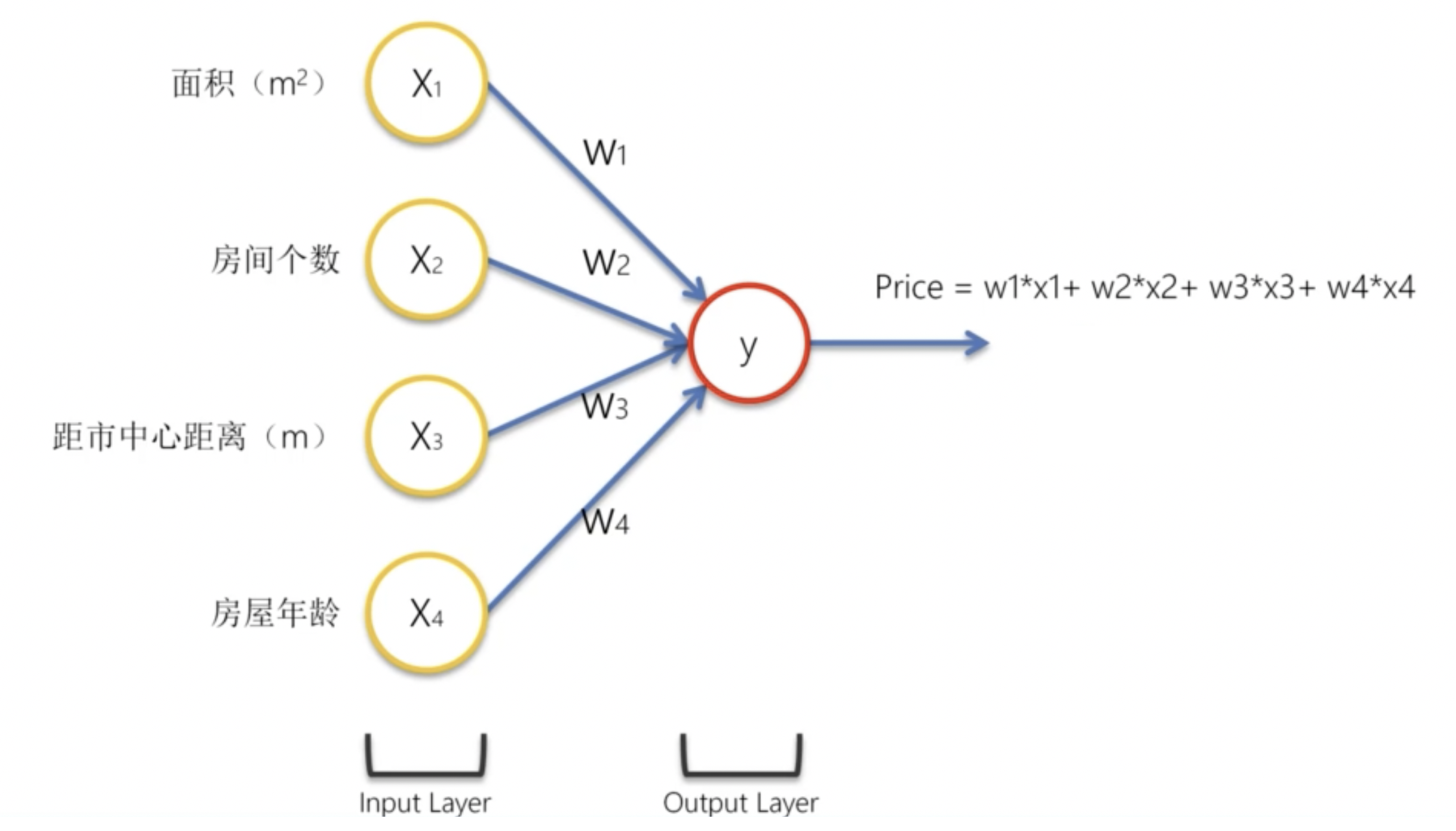
我們為其添加隱藏層神經元:
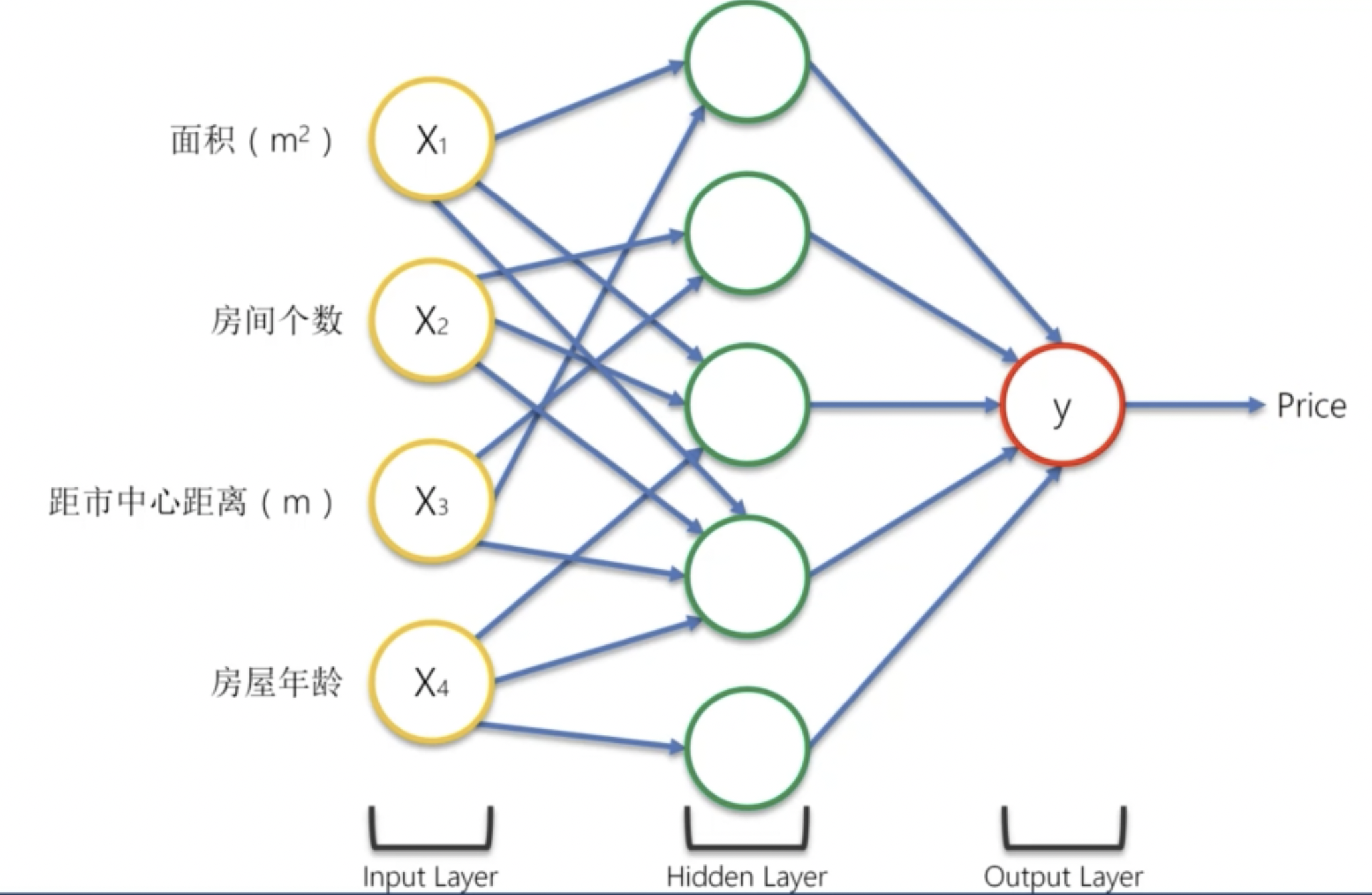
並非所有的輸入都對每一個隱藏神經元有影響。對該神經元沒有影響的輸入,我們可以將其權重看做 0。
比如,對於第一個隱藏神經元,僅有房屋面積和距離市中心的距離對其有影響。那麼這個神經元代表什麼呢?
我們可以想一下,在房價差不多的情況下,一般距離市中心越遠,房屋面積就越大。因此,在房價差不多的情況下,房屋面積和距離市中心的距離是有關聯的。這個神經元可能就是用來表示這種關聯的。
神經網路的學習方式
解決問題的方式在根本上有兩種:指令式程式設計和學習式程式設計。指令式程式設計是我們平常所用的程式設計方式,也就是我們告訴電腦怎麼做。而學習式程式設計則是讓電腦自己學習,然後根據學習的結果來做決策。
我們先來搭建這樣一個最簡單的神經網路框架:
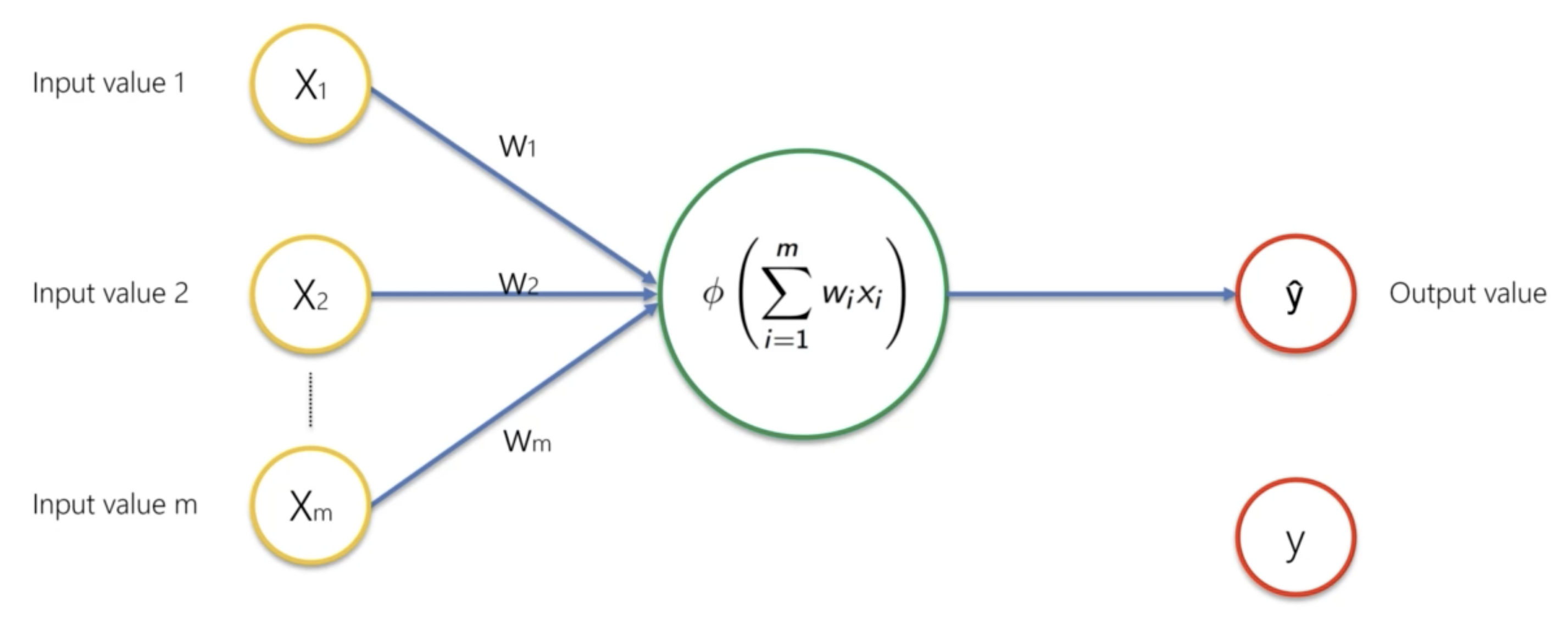
圖中的 指的是我們透過模型預測的輸出, 指的是真實的輸出。我們的目標是使得 越接近 越好。
我們把這個最簡單的神經網路模型叫做感知器(Perceptron)。
當我們透過一系列隱藏層和輸出層,獲得預測結果 之後,我們需要計算這個預測結果和真實結果之間的差距。這個差距我們稱之為損失函數(Loss Function)。損失函數的選擇是非常重要的,它直接影響到我們的模型的性能。因此,我們的模型優化問題就被轉化為了損失函數的最小化問題。
而後,我們將透過**反向傳播(Backpropagation)**算法來調整我們的權重和偏差,使得損失函數最小化。
梯度下降算法
梯度下降算法是一種用於最小化損失函數的優化算法。梯度下降算法的核心思想是:對於一個函數 ,我們希望找到一個 ,使得 的值最小。我們可以透過計算 的梯度來找到這個 。
我們已經知道,我們可以透過更新權重和偏差來最小化損失函數。我們可以想到的最簡單的思路就是充分利用機器的計算性能,即傻瓜式試驗。比如,如果我們有 25 個權重,想要試驗 1000 次,那我們只需要計算 次即可⋯⋯
等等,多少??這顯然是一個天文數字!這種情況,在圈內有一個專門的名稱,叫做 Curse of Dimensionality —— 維度災難。這種情況下,我們的計算量是非常大的,而且很有可能會陷入局部最小值。因此,我們需要一種更加高效的算法來解決這個問題。解決問題的辦法顯然就是梯度下降算法。
梯度下降算法的核心模擬:如果我們將損失函數看做一個碗,我們的目標就是找到這個碗的最低點。我們可以想像,當我們站在這個碗的某一點,我們會向下走,直到找到這個碗的最低點。那麼我們站在這個點上,如何決定往哪裡走呢?答案是沿著切線的方向。我們發現,在損失函數上的任意一個點,其切線方向永遠是下降的方向。因此,我們可以沿著梯度的方向,來更新我們的權重和偏差。
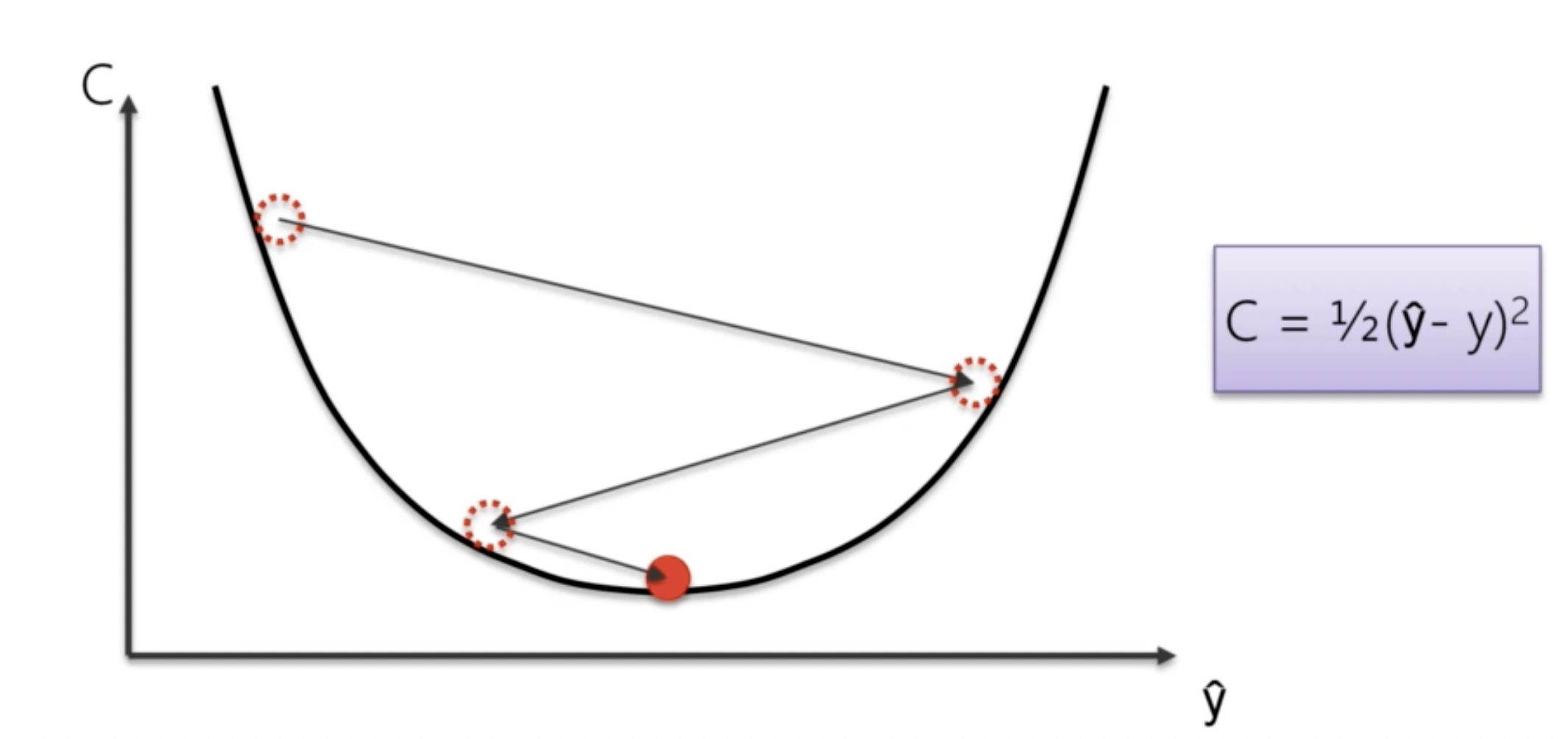
隨機梯度下降算法
隨機梯度下降可以看作是梯度下降算法的加強版。
如果我們的資料數量比較多,那我們傳統的梯度下降算法是這樣解決的:只有當所有的資料都已經完成了一次迭代之後,我們才可以透過 來計算總損失函數,才可以應用梯度下降算法做反向傳播。這顯然是非常耗時的。
隨機梯度下降算法的核心思想是:每次只取一個樣本來計算損失函數,然後進行反向傳播。權重更新完成之後,我們再取下一個樣本。每一個樣本都有對模型進行一次完整的迭代。
卷積神經網路 CNN
卷積神經網路是一種用於圖像識別的神經網路。比如現在十分流行的 Face ID 等技術,就是基於卷積神經網路的例子。筆者作為臨床醫學專業人員,卷積神經網路對筆者的工作也有很大的幫助,比如醫學影像識別等。
我們首先認識一下圖片在電腦中到底是什麼。比如,我們有一張黑白圖片,這張圖片是由一個個像素點組成的。每個像素點都有一個灰度值,這個灰度值代表了這個像素點的顏色。我們可以將這個灰度值看做是一個矩陣,這個矩陣的大小就是圖片的大小。比如,一張 28x28 的圖片,就是一個 28x28 的矩陣。
而彩色圖片則可以被看做是一個三維矩陣,分別是長、寬和深度。深度指的是 RGB 三個通道。
卷積層
什麼是卷積?卷積是一種數學運算,用於圖像處理。卷積運算的核心思想是:將一個小的矩陣(稱為卷積核)在一個大的矩陣上滑動,並計算兩個矩陣的內積。這樣,我們就可以得到一個新的矩陣。
關於卷積算法的數學定義,實在太過複雜,這裡不便詳述。
比如,我們有如下一個卷積計算過程:
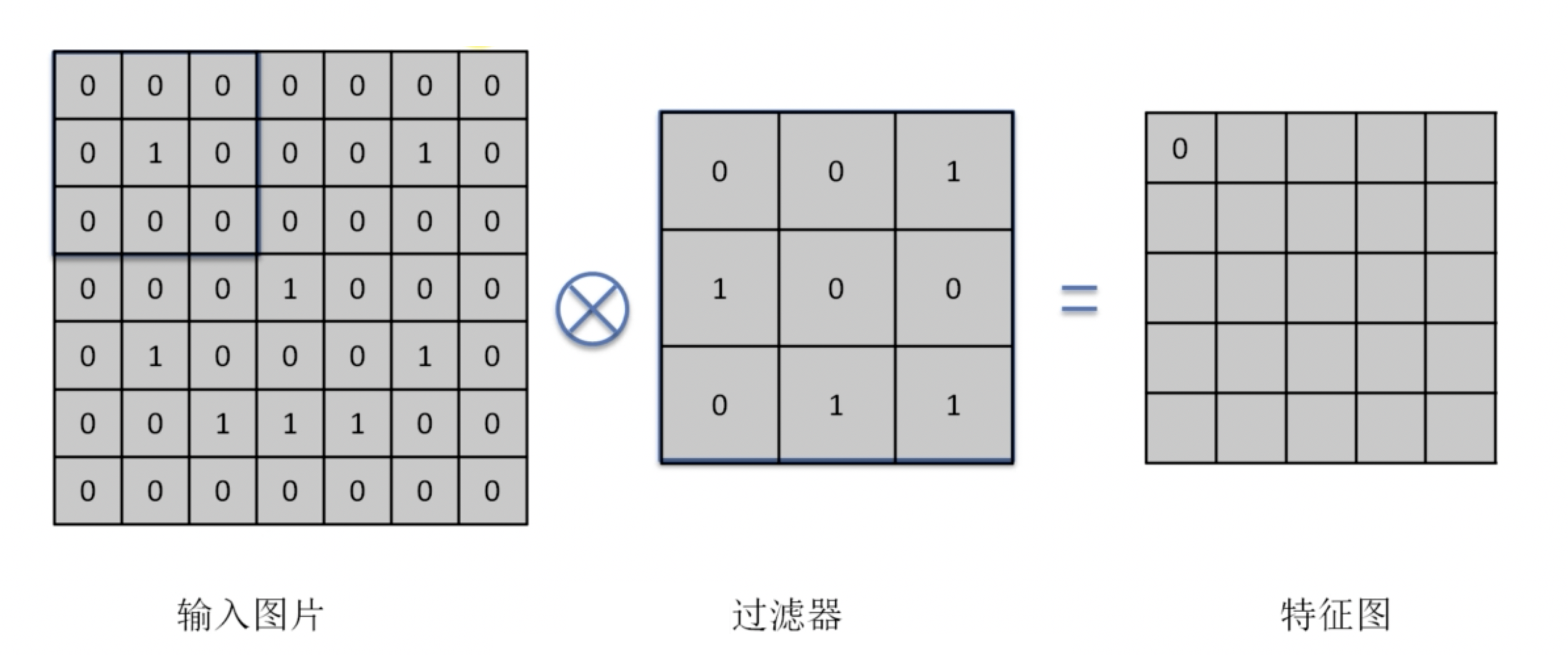
我們可以看到,卷積運算的核心是內積的運算。這種運算是:將兩個矩陣對應位置的元素相乘,然後將這些乘積相加。
而後我們將卷積核向右滑動一個單位,再次進行內積運算。如此反覆,這樣,我們就可以得到一個新的矩陣。比較好的卷積核的大小是 到 的大小。當然,我們的步頻也是可以調整的。
經過幾層卷積層之後,我們可以得到一些非常抽象的特徵集合。在實際的應用中,我們會得到許多張特徵圖,這些特徵圖是透過使用不同的卷積核得到的。
ReLU 層
當我們得到了特徵圖之後,我們需要對這些特徵圖進行激勵。這時,我們就需要使用 ReLU 層。ReLU 層使用 ReLU 函數作為激勵函數。
最大池化層
最大池化層是一種用於減少特徵圖大小的層。最大池化層的核心思想是:將一個特徵圖分成多個小的區域,然後取每個區域的最大值。這樣,我們就可以得到一個新的特徵圖。
這個過程在做什麼?這個過程可以探測出圖像中特徵的相對位置,還可以避免圖片的過度擬合。
扁平化
在最大池化層之後,我們需要將特徵圖扁平化。這樣,我們就可以得到一個向量,這個向量可以作為我們的輸入。
扁平化的過程十分簡單,就是將特徵圖矩陣拉成一條向量。
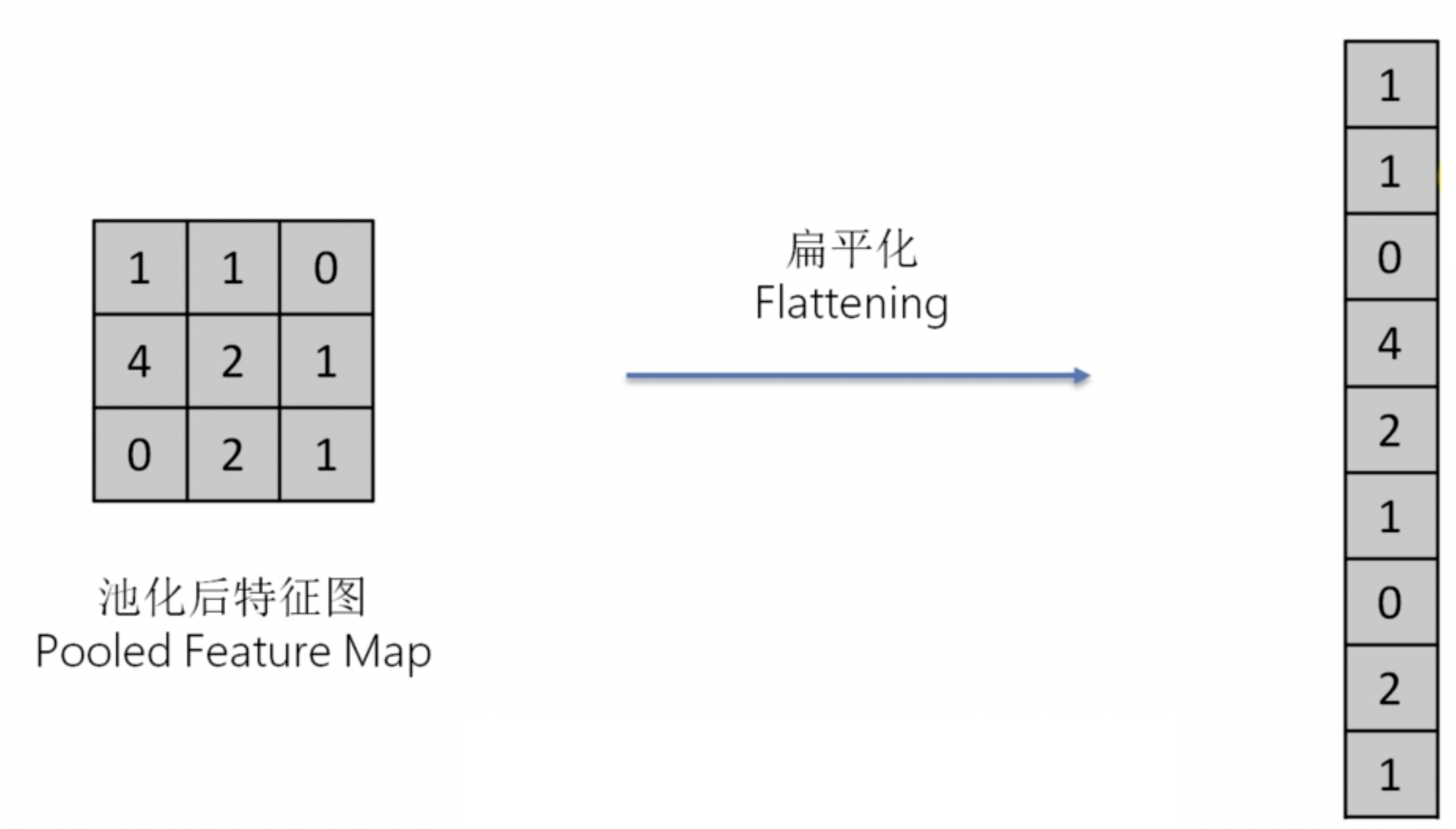
全連接層
全連接層指的是在神經網路的每一層神經元都和上一層的所有神經元相連。全連接層是一種用於將特徵圖轉換為輸出的層。事實上,上一步扁平化之後得到的 vector,就是全連接層的輸入。而全連接層事實上就是一個類神經網路。
降維
降維是一種用於減少特徵數量,即自變數之數量的技術。降維的目的是:減少計算量、減少過度擬合、提高模型的準確性。
我們介紹兩種降維算法:主成分分析(PCA)和核函數主成分分析(Kernel PCA)。
主成分分析 PCA
主成分分析是一種用於降維的技術。PCA 的核心思想是:將原始資料投影到一個新的坐標系統中,使得投影後的數據的變異數最大。
在我們運用 PCA 的時候,我們需要找到“最大變異數所屬方向”。
我們直接使用 Python 實現一個 PCA:
from sklearn.decomposition import PCA
pca = PCA(n_components = 2) # 降維到 2 維
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)核函數主成分分析 Kernel PCA
核函數主成分分析是一種用於非線性降維的技術。Kernel PCA 的核心思想是:將原始資料投影到一個新的高維空間中,使得投影後的數據的變異數最大。
我們直接使用 Python 實現一個 Kernel PCA:
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(n_components = 2, kernel = 'rbf') # 降維到 2 維
X_train = kpca.fit_transform(X_train)
X_test = kpca.transform(X_test)模型選擇和性能優化
在機器學習中,我們需要選擇一個合適的模型。模型的選擇是非常重要的,它直接影響到我們的模型的性能。
超參數,是指我們在訓練模型時需要設置的參數。比如,我們在訓練一個決策樹模型時,我們需要設置樹的深度、節點的最小樣本數等等,它們與我們的樣本自變數無關。這些參數就是超參數。
我們可以用更好的方法來選擇這些超參數。
交叉驗證
我們首先將 dataset 分成十份,然後進行十次交叉驗證。在第一次驗證時,我們將第一份作為驗證集,其餘九份作為訓練集,得到一個擬合完成的模型。在第二次驗證時,我們將第二份作為驗證集,其餘九份作為訓練集。如此反復,直到第十次驗證,我們得到了十個模型和十個準確率。
而後,我們取這十個準確率的平均值,作為我們的模型的準確率。
我們在 Python 中實現交叉驗證:
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator = classifier, X = X_train, y = Y_train, cv = 10) # cv 是交叉驗證的次數
mean = accuracies.mean()
std = accuracies.std()網格檢索
網格檢索是一種用於選擇超參數的技術。網格檢索的核心思想是:我們先設置一個超參數的範圍,然後對這個範圍內的每一個超參數進行訓練,然後選擇最好的超參數。
我們在 Python 中實現網格檢索:
from sklearn.model_selection import GridSearchCV
parameters = [{'C': [1, 10, 100, 1000], 'kernel': ['linear']}, {'C': [1, 10, 100, 1000], 'kernel': ['rbf'], 'gamma': [0.5, 0.1, 0.01, 0.001, 0.0001]}] # 超參數的範圍
grid_search = GridSearchCV(estimator = classifier, param_grid = parameters, scoring = 'accuracy', cv = 10, n_jobs = -1) # n_jobs 是使用的 CPU 核心數,-1 表示使用所有核心
grid_search = grid_search.fit(X_train, Y_train)
best_accuracy = grid_search.best_score_
best_parameters = grid_search.best_params_結束了嗎?
這篇文章是對《機器學習 A-Z》課程的一個總結。這門課程是一門非常好的機器學習入門課程,它涵蓋了機器學習的基礎知識,並且通過實際的案例來展示這些知識。這門課程的一個缺點是:它的內容比較老,使用的框架也比較老。但是,這並不影響這門課程的價值。感謝武亦文(Yiwen)和李秦(Qin)老師的教學!
文章結束了,課程結束了,但是歡迎自己,也歡迎本文的讀者正式進入機器學習的神奇世界。機器學習是一個非常有趣的領域,它可以幫助我們解決許多現實生活中的問題。希望本文能夠幫助到你,也希望你能夠在機器學習的道路上越走越遠!
本文應該是本部落格開文以來最長的文章了,也感謝您能夠看到這裡。接下來,筆者將會繼續探究深度學習、機器視覺、影像組學等領域的知識,並在之後的文章中進行更深入的探討。敬請期待!