技術文章
深度學習
PyTorch
圖像分類
CNN

[深度學習] 從幾個示例系統學習 PyTorch 的應用（超長文預警）

2024 年 10 月 29 日
文章摘要
FakeGPT
加載中...
此內容由人工不智慧生成。

安裝

造訪 PyTorch 官網，往下滑動，看到這個了沒？

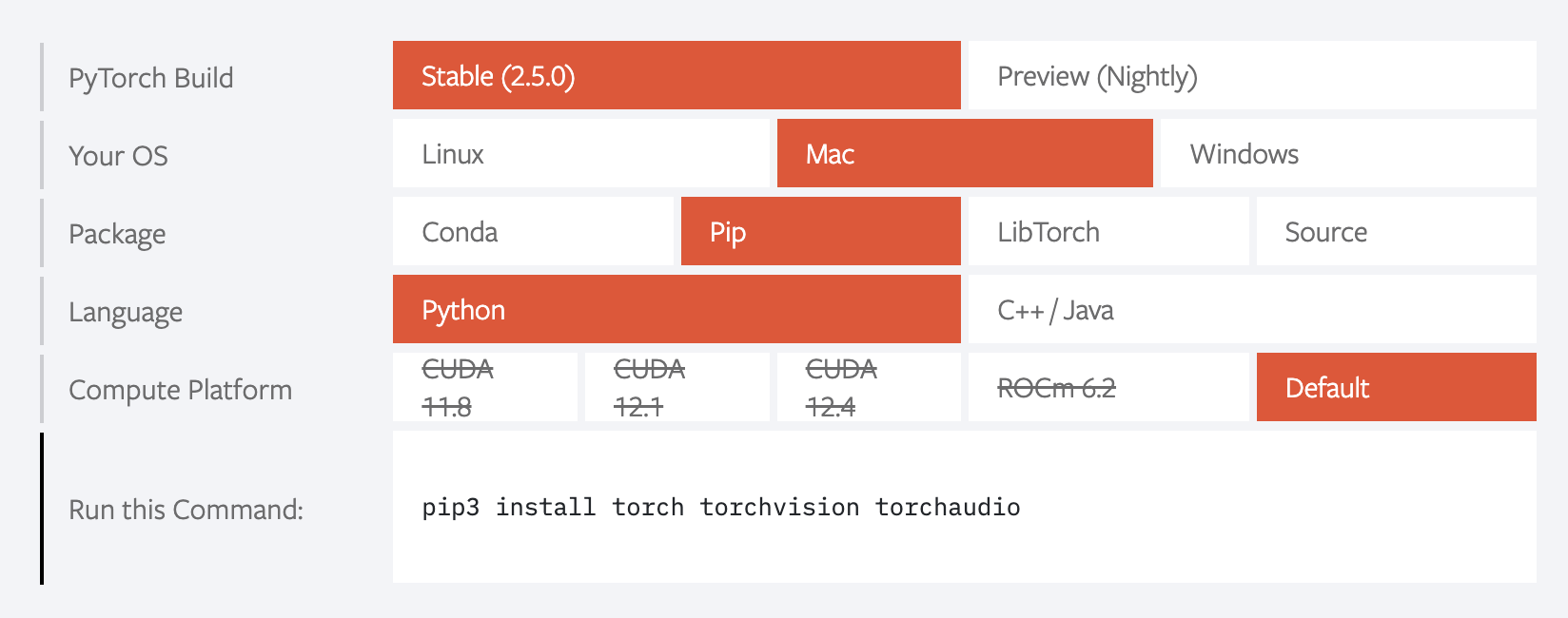
懂了吧？好，我們繼續。

PyTorch Fundamentals: Tensor

Tensor，中文名稱為張量，是 PyTorch 中最基本的數據結構。它是一個多維陣列，支持 GPU 加速運算。在 PyTorch 中，Tensor 類似於 NumPy 的 ndarray。

Tensor 可以分為 Scalar（純量，零維）、Vector（向量，一維）、Matrix（矩陣，二維）和 N-Dimensional Array（多維陣列，N 維）。

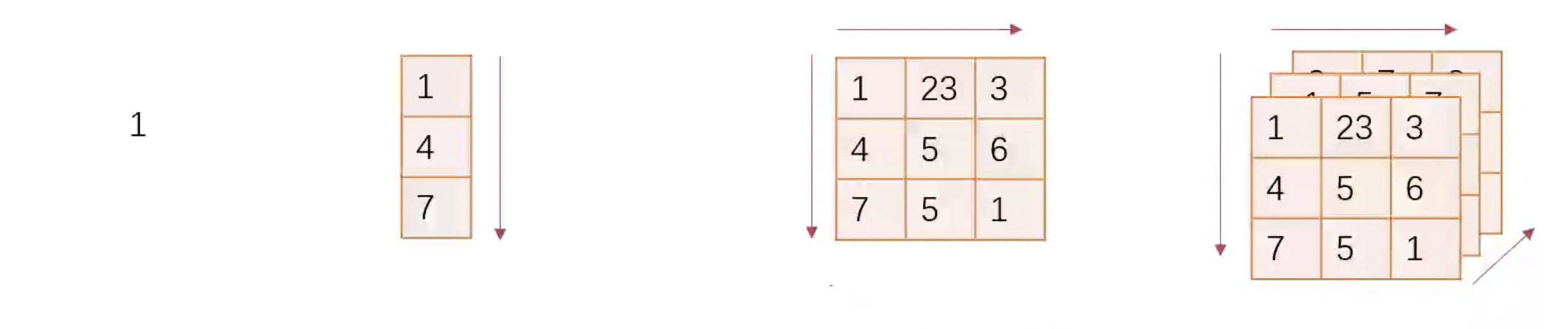
創建 Tensor

創建 Tensor 有幾種不同的方法。

首先，我們可以使用 torch.tensor() 函數從 Python 數據直接創建 Tensor。

import torch


# 創建一個 1D Tensor
list = [1, 2, 3, 4, 5]
tensor1d = torch.tensor(list)


# 創建一個 2D Tensor
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
tensor2d = torch.tensor(matrix)


print(tensor1d)
# tensor([1, 2, 3, 4, 5])
print(tensor2d)
# tensor([[1, 2, 3],
#         [4, 5, 6],
#         [7, 8, 9]])

我們還可以使用 torch.from_mumpy() 從 NumPy 創建 Tensor。

import numpy as np


# 創建一個 NumPy ndarray
ndarray = np.array([1, 2, 3, 4, 5])


# 將 NumPy ndarray 轉換為 Tensor
tensor = torch.from_numpy(ndarray)


print(tensor)
# tensor([1, 2, 3, 4, 5])

需要注意的是，torch.from_numpy() 創建的 Tensor 和原始 NumPy ndarray 共享記憶體，因此修改其中一個將影響另一個。

其他的方法，我們可以使用 torch.zeros()、torch.ones()、torch.rand() 等函數創建特定形狀的 Tensor。

# 創建一個 3x3 的全零 Tensor
zeros = torch.zeros(3, 3)


# 創建一個 3x3 的全一 Tensor
ones = torch.ones(3, 3)


# 創建一個 3x3 的隨機 Tensor
rand = torch.rand(3, 3)


print(zeros)
# tensor([[0., 0., 0.],
#         [0., 0., 0.],
#         [0., 0., 0.]])
print(ones)
# tensor([[1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.]])
print(rand)
# tensor([[0.1234, 0.2345, 0.3456],
#         [0.4567, 0.5678, 0.6789],
#         [0.7890, 0.8901, 0.9012]])

我們以 torch.zeros() 為例，看一下它們的參數。

torch.zeros(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) -> Tensor
  • size：Tensor 的形狀。
  • out：輸出 Tensor。值為 None 或一個 Tensor。當值為 Tensor 時，將會把結果存儲到這個 Tensor 中。out 所指的 Tensor 與原始 Tensor 共享記憶體。
  • dtype：Tensor 的數據類型。
  • layout：Tensor 的佈局。預設是 torch.strided，當矩陣是稀疏矩陣時，可以使用 torch.sparse_coo。
  • device：Tensor 所在的裝置。
  • requires_grad：是否需要計算梯度。

其他的生成方法使用得相對較少，這裡就不一一介紹。

Tensor 的操作

Tensor 支援多種操作，包括數學運算、索引和切片、形狀操作等。

拼接

我們可以使用 torch.cat() 或者 torch.stack() 將多個 Tensor 拼接在一起。

import torch


# 創建兩個 2D Tensor
tensor1 = torch.tensor([[1, 2, 3], [4, 5, 6]])
tensor2 = torch.tensor([[4, 5, 6], [7, 8, 9]])


# 將兩個 Tensor 拼接在一起
cat = torch.cat((tensor1, tensor2), dim=0)


# 將兩個 Tensor 堆疊在一起
stack = torch.stack((tensor1, tensor2), dim=0)


print(cat)
# tensor([[1, 2, 3],
#         [4, 5, 6],
#         [4, 5, 6],
#         [7, 8, 9]])


print(stack)
# tensor([[[1, 2, 3],
#          [4, 5, 6]],
#         [[4, 5, 6],
#          [7, 8, 9]]])

我們可以看到，torch.cat() 會保留原始 Tensor 的維度，而 torch.stack() 會增加一個新的維度。注意，只有當兩個 Tensor 的形狀完全一致時，torch.stack() 才能正確執行，而 torch.cat() 只需要保證拼接的維度相同即可。

切分

我們可以使用 torch.split() 或者 torch.chunk() 將一個 Tensor 切分成多個 Tensor。

import torch


# 創建一個 2D Tensor
tensor = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])


# 將 Tensor 切分成兩個 Tensor
split = torch.split(tensor, 1, dim=0) # 1 表示每個 Tensor 的大小


# 將 Tensor 切分成兩個 Tensor
chunk = torch.chunk(tensor, 2, dim=0) # 2 表示切分的個數


print(split)
# (tensor([[1, 2, 3]]), tensor([[4, 5, 6]]), tensor([[7, 8, 9]]))


print(chunk)
# (tensor([[1, 2, 3],
#         [4, 5, 6]]), tensor([[7, 8, 9]]))

torch.split() 和 torch.chunk() 的區別在於，torch.split() 按照指定的大小切分，而 torch.chunk() 按照指定的個數切分。

索引

我們可以使用索引來訪問 Tensor 中的元素。

import torch


# 創建一個 2D Tensor
tensor = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])


# 訪問第一行第一列的元素
element = tensor[0, 0]


print(element)
# tensor(1)

還可以使用 toroch.index_select() 或 torch.masked_select() 來進行索引。

import torch


# 創建一個 2D Tensor
tensor = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])


# 使用 index_select() 選取第一行和第三行
indices = torch.tensor([0, 2])


selected = torch.index_select(tensor, dim=0, indices)


mask = tensor.ge(5) # 大於等於 5 的元素
masked = torch.masked_select(tensor, mask)


print(selected)
# tensor([[1, 2, 3],
#         [7, 8, 9]])


print(masked)
# tensor([5, 6, 7, 8, 9])

torch.index_select() 選取指定的行列，torch.masked_select() 選取符合條件的元素，回傳一維 Tensor。

轉置

torch.reshape() 可以用來改變 Tensor 的形狀。

import torch


# 創建一個 2D Tensor
tensor = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])


# reshape
reshaped = torch.reshape(tensor, (3, 4))


print(reshaped)
# tensor([[ 1,  2,  3,  4],
#         [ 5,  6,  7,  8],
#         [ 9, 10, 11, 12]])

可以使用 torch.t() 或 torch.transpose() 來進行轉置。其中，torch.t() 只能用於 2D Tensor，相當於 torch.transpose() 的簡化版。

import torch


# 創建一個 2D Tensor
tensor = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])


# 轉置
td = torch.t(tensor)


transposed = torch.transpose(tensor, 0, 1) # 0 和 1 表示維度


print(td)
# tensor([[1, 4, 7],
#         [2, 5, 8],
#         [3, 6, 9]])


print(transposed)
# tensor([[1, 4, 7],
#         [2, 5, 8],
#         [3, 6, 9]])

三種轉置操作生成的新 Tensor 與原 Tensor 共享記憶體。

數學運算

看圖（大多數人應該都可以讀懂簡中吧⋯⋯）：

Tensor 的 GPU 加速

PyTorch 支援 GPU 加速運算，可以使用 torch.cuda.is_available() 檢查是否有可用的 GPU。注意，如果你和筆者一樣使用的是 Apple Silicon 的 Mac 的話，是 mps 而不是 cuda。

import torch


# 獲取計算裝置
device = torch.device('cuda' if torch.cuda.is_available() else 'mps' if torch.mps.is_available() else 'cpu') # 哪一個可用就使用哪一個


# 創建一個 Tensor
tensor = torch.tensor([1, 2, 3, 4, 5])


# 將 Tensor 移動到 GPU
tensor = tensor.to(device)


print(tensor)
# tensor([1, 2, 3, 4, 5], device='mps:0')

資料預處理

在深度學習中，資料預處理是非常重要的一個步驟。在進行模型訓練之前，我們需要將原始資料轉換為模型可以接受的格式。我們的資料可能千奇百怪，比如二維圖像、普通表格、自然語言文本等，我們需要將這些資料轉換為 Tensor，並進行標準化、正規化等操作。

二維圖像的 Load

我們首先要理解圖像的基本構成。圖像是由像素組成的，每個像素包含了顏色信息。如果是灰度圖像，每個像素只有一個值，表示亮度；如果是彩色圖像，每個像素有三個值，分別表示R、G、B三個通道的亮度。

我們使用 imageio 這個 Package 來讀取圖像。

import imageio.v3 as im


# Load image
img = im.imread('image.jpg')


print(img.shape)
# (H, W, C)

img 是一個三維的 NumPy ndarray，其中 H 表示圖像的高度，W 表示圖像的寬度，C 表示通道數。如果是灰度圖像，C 為 1；如果是彩色圖像，C 為 3。

接下來，我們將圖像轉換為 Tensor。

import torch


# Convert image to tensor
tensor = torch.from_numpy(img)


# Permute the dimensions
tensor = tensor.permute(2, 0, 1) # 將 C 放到第一個維度


print(tensor.shape)
# (C, H, W)

這樣產生的 Tensor，第一維中每一個元素代表一個 Pixel 點位。

我們也可以批量處理圖像，將多個圖像轉換為 Tensor。

import imageio


# Load images
img1 = imageio.imread('image1.jpg')
img2 = imageio.imread('image2.jpg')
img3 = imageio.imread('image3.jpg')


# Convert images to tensor
batch_size = 3 # 圖片的數量
batch = torch.zeros((batch_size, img1.shape[2], img1.shape[0], img1.shape[1]), dtype=torch.uint8) # 創建一個 batch


batch[0] = torch.from_numpy(img1).permute(2, 0, 1)


batch[1] = torch.from_numpy(img2).permute(2, 0, 1)


batch[2] = torch.from_numpy(img3).permute(2, 0, 1)


print(batch.shape)
# (B, C, H, W)

普通表格的 Load

普通表格是一種二維的資料結構，每一列代表一個樣本，每一欄代表一個特徵。我們可以使用 pandas 來讀取表格資料。

import pandas as pd


# Load data
data = pd.read_csv('data.csv')


# 將 DataFrame 轉換為 Tensor
tensor = torch.tensor(data.values)


print(tensor.shape)


# (N, M)

data 是一個 DataFrame，data.values 是一個二維的 NumPy ndarray，其中 N 表示樣本數，M 表示特徵數。

其他的表格處理，請參考我的上一篇文章《機器學習 A-Z 學習筆記（超長文預警）》的資料預處理部分，包括如何處理分類資料。

自然語言文本的 Load

對於這部分內容，我的上一篇文章《機器學習 A-Z 學習筆記（超長文預警）》有詳細的介紹，這裡就不再贅述。

3D 影像的 Load

我們之後的例子是一個影像組學的預測案例，使用到的是 CT 圖像。這裡為沒有醫學專業背景的讀者解釋一下，CT 圖像是一種三維的影像，由許多張平面的掃描影像經過電腦重新組合建模而成。這類圖像文件的格式通常是 DICOM，這是一個醫學數字成像和通信標準。我們仍然可以使用 imageio 來讀取這類圖像。

import imageio


# Load 3D image
img = imageio.volread('image.dcm', 'DICOM')


print(img.shape)
# (D, H, W)

img 是一個三維的 NumPy ndarray，其中 D 表示深度，H 表示高度，W 表示寬度。

接下來，我們將 3D 影像轉換為 Tensor。

import torch


# Convert 3D image to tensor
tensor = torch.from_numpy(img)


# Permute the dimensions
tensor = tensor.permute(0, 2, 1) # 將 H 和 W 交換


print(tensor.shape)
# (D, W, H)

這樣產生的 Tensor，第一維中每一個元素代表一個 2D 影像。

透過簡單的溫度轉換示例看 PyTorch 的模型訓練、評估、優化

這裡我們使用一個簡單的溫度轉換的案例來展示 PyTorch 的模型訓練、評估和優化。在我們大多數的國家，溫度都使用攝氏溫度，但是有些國家，比如美國，使用華氏溫度。我們的任務是訓練一個模型，能夠找到攝氏溫度與華氏溫度的規律，並且能夠實現溫度的互相轉換。

常規模型的訓練過程

我們將數據輸入到我們的模型中，並且預測結果，然後將預測結果與真實結果進行比較，計算損失。我們使用梯度下降法來做權重修正，優化模型，使得損失最小化。

之於我們上一個例子，我們使用下面的步驟來實現：

  1. 收集一批示數數據
  2. 假設一個模型公式
  3. 把數據輸入模型
  4. 計算出一組模型的權重
  5. 使用模型預測結果並與已知結果對比
  6. 根據差距迭代權重

我們一步一步來看，先做前兩步。

# 1. 收集一批示數數據
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0] # 已知的攝氏溫度


t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4] # 未知的溫度


# 轉換為 Tensor
t_c = torch.tensor(t_c)
t_u = torch.tensor(t_u)


# 2. 假設一個模型公式
# 假設模型公式為 t_c = w * t_u + b，其中 w 是權重，b 是偏置
def model(t_u, w, b):
    return w * t_u + b

損失函數

損失函數是用來衡量模型預測結果與真實結果之間的差距。損失函數的定義和選擇對於模型的訓練和優化至關重要。在這個例子中，我們使用均方誤差（Mean Squared Error，MSE）作為損失函數。它的公式可以表示為：

Loss=(tp−tc)2Loss = (t_p - t_c)^2

def loss_fn(t_p, t_c):
    squared_diffs = (t_p - t_c) ** 2
    return squared_diffs.mean()

我們繼續我們的過程：

# 3. 把數據輸入模型
# 初始化權重和偏置
w = torch.ones(())
b = torch.zeros(())


# 輸入模型
t_p = model(t_u, w, b)


# 計算誤差
loss = loss_fn(t_p, t_c)

梯度

梯度是損失函數對於權重和偏置的偏導數。我們使用梯度下降法來優化模型，使得損失最小化。關於梯度下降演算法，請參考我的上一篇文章《機器學習 A-Z 學習筆記（超長文預警）》。

關於梯度的數學計算，給出公式：

∇L=(∂L∂w,∂L∂b)\nabla L = \left(\frac{\partial L}{\partial w}, \frac{\partial L}{\partial b}\right)

根據鏈式微分法則，我們可以得到：

∇L=(∂L∂model⋅∂model∂w,∂L∂model⋅∂model∂b)\nabla L = \left(\frac{\partial L}{\partial model}\cdot \frac{\partial model}{\partial w}, \frac{\partial L}{\partial model}\cdot \frac{\partial model}{\partial b}\right)

不要問公式是哪裡來的！由於筆者那驚天地泣鬼神的數學能力，這裡顯然不知道。我們只需要知道，為了計算梯度，我們需要計算損失函數對於模型的偏微分∂L∂model\frac{\partial L}{\partial model} 和模型對於權重和偏置的偏微分∂model∂w\frac{\partial model}{\partial w} 和∂model∂b\frac{\partial model}{\partial b}。

def dloss_fn(t_p, t_c):
    dsq_diffs = 2 * (t_p - t_c) / t_p.size(0)
    return dsq_diffs


def dmodel_dw(t_u, w, b):
    return t_u


def dmodel_db(t_u, w, b):
    return 1.0

好了！到此為止了！不要再去深究了！因為 PyTorch 有一個強大的自動微分系統，可以幫助我們自動計算梯度。因此這裡只是寫來玩一玩，不要太認真！（卑微數學渣渣在線求饒）

我們繼續梯度計算：

def grad_fn(t_u, t_c, t_p, w, b):
    dloss_dtp = dloss_fn(t_p, t_c)
    dloss_dw = dloss_dtp * dmodel_dw(t_u, w, b)
    dloss_db = dloss_dtp * dmodel_db(t_u, w, b)
    return torch.stack([dloss_dw.sum(), dloss_db.sum()])

學習率

學習率是梯度下降法中的一個重要參數，它決定了每次迭代中權重和偏置的更新幅度。學習率太大會導致震盪，學習率太小會導致收斂速度過慢。在實際應用中，我們需要通過實驗來選擇合適的學習率。

通常經驗來說，在剛開始的時候，學習率可以設置得比較大，0.01～0.001 即可，然後隨著訓練的進行，逐漸減小。這樣可以加快模型的收斂速度，同時又不會過度震盪。

# 4. 5. 6.
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        w, b = params


        t_p = model(t_u, w, b)
        loss = loss_fn(t_p, t_c)
        grad = grad_fn(t_u, t_c, t_p, w, b)


        params = params - learning_rate * grad


        print('Epoch %d, Loss %f' % (epoch, float(loss)))


    return params

我們來看一下訓練過程：

params = training_loop(
    n_epochs = 5000,
    learning_rate = 1e-2,
    params = torch.tensor([1.0, 0.0]),
    t_u = t_u,
    t_c = t_c
)

恭喜，你已經成功訓練了一個模型！先為自己鼓掌吧！完整的程式碼如下：

import torch


# 1. 收集數據
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]


t_c = torch.tensor(t_c)
t_u = torch.tensor(t_u)


# 2. 假設模型和損失函數
def model(t_u, w, b):
    return t_u * w + b


def loss_fn(t_p, w, b):
    return ((t_p - t_c) ** 2).mean()


# 3. 數據輸入
w = torch.ones(())
b = torch.zeros(())


t_p = model(t_u, w, b)


# 4. 梯度下降，反向傳播
def dloss_fn(t_p, t_c):
    return 2 * (t_p - t_c) / t_p.size(0)


def dmodel_dw(t_u, w, b):
    return t_u


def dmodel_db(t_u, w, b):
    return 1.0


def grad_fn(t_u, t_c, t_p, w, b):
    dloss_dtp = dloss_fn(t_p, t_c)
    dloss_dw = dloss_dtp * dmodel_dw(t_u, w, b)
    dloss_db = dloss_dtp * dmodel_db(t_u, w, b)
    return torch.stack([dloss_dw.sum(), dloss_db.sum()])


def training_loop(n_epochs, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        w, b = params
        t_p = model(t_u, w, b)
        loss = loss_fn(t_p, w, b)
        grad = grad_fn(t_u, t_c, t_p, w, b)


        params = params - learning_rate * grad


        print('Epoch %d, Loss %f' % (epoch, float(loss)))


    return params


if __name__ == '__main__':
    params = training_loop(
        n_epochs=1000,
        learning_rate=1e-5,
        params=torch.tensor([1.0, 0.0]),
        t_u=t_u,
        t_c=t_c,
    )


    print(params)

歸一化

先把我們自己從模型成功運行的喜悅中拔出來，我們來仔細看一下我們的這個模型，是否還有什麼問題？有的，我們發現，最後訓練 1000 次之後的權重和偏置分別是 0.2327 和 -0.0438，它們差不多有 10 倍的差距。這樣，當我們使用同一個 learning rate，可能會導致權重和偏置的更新速度不一致，進而影響模型的訓練效果。

考慮到成本的問題，我們不太可能對於每一個參數都設定一個單獨的 learning rate，因此我們需要對數據進行歸一化處理。歸一化的目的是將數據縮放到一個合理的範圍內，使得不同特徵之間的差異不會影響模型的訓練效果。

一個歸一化的公式是：

x′=x−μσx' = \frac{x - \mu}{\sigma}

有學過統計學的朋友應該知道這個公式，其中 xx 是原始數據，μ\mu 是平均值，σ\sigma 是標準差。這樣，我們就可以將數據歸一化到均值為 0，標準差為 1 的範圍內。

歸一化有很多好處，比如可以加快模型的收斂速度，提高模型的準確性，減少過擬合等。當然，歸一化也有一些缺點，比如可能會導致模型的解釋性下降，使得模型的可解釋性變差。

使用 PyTorch 的自動微分系統

來了！這個英雄它來了！拯救一個數學渣渣於水火的 PyTorch 自動微分系統！這個系統可以幫助我們自動計算梯度，不需要我們手動計算梯度，這樣就大大簡化了我們的工作。

# 令參數可自動微分
params = torch.tensor([1.0, 0.0], requires_grad=True) # 設置 requires_grad=True


# 4. 5. 6.
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        # 清空梯度，背下來就好
        if params.grad is not None:
            params.grad.zero_()


        t_p = model(t_u, *params)
        loss = loss_fn(t_p, t_c)
        loss.backward()


        with torch.no_grad():
            params -= learning_rate * params.grad


        if epoch % 500 == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))


    return params

模型優化

首先是超參數優化。對於超參數的概念，即我們模型中需要人工配置的未知參數，比如 learning rate，比如 epoch，比如 batch size 等等。

對於超參數的選擇，我們可以使用網格搜索、隨機搜索、貝葉斯優化等方法。

此外，我們可以使用 PyTorch 為我們提供的優化器來優化模型。優化器位於 torch.optim。

optimizer = optim.SGD([params], lr=learning_rate)

然後，我們就可以使用 optimizer 來手動歸零梯度，以及更新權重了。

def training_loop(n_epochs, optimizer, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        t_p = model(t_u, *params)
        loss = loss_fn(t_p, *params)
        optimizer.zero_grad() # 手動梯度歸零
        loss.backward()
        optimizer.step() # 自動更新權重


        print('Epoch %d, Loss %f' % (epoch, float(loss)))


    return params

激勵函數

激勵函數是神經網路中的一個重要組件，它決定了神經元的輸出。常見的激勵函數有 Sigmoid、Tanh、ReLU 等。如果你想詳細了解不同的激勵函數，歡迎訪問我上一篇文章《機器學習 A-Z 學習筆記（超長文預警）》。

激勵函數可以為神經網路添加非線性，使得神經網路可以學習更加複雜的模式。我們可以認為，一個神經元，就是一個線性變換 + 一個激勵函數構成。

使用 torch.nn 模組構建線性模型

# 1. 收集數據
import torch


t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]


t_c = torch.tensor(t_c).unsqueeze(1) # 升維，作用是將資料轉化成單個樣本
t_u = torch.tensor(t_u).unsqueeze(1)


n_samples = t_u.shape[0] # 樣本量
n_test = int(n_samples * 0.2) # 測試集數量


shuffled_samples = torch.randperm(n_samples) # 隨機化樣本


train_indics = shuffled_samples[:-n_test] # 訓練集索引
test_indics = shuffled_samples[n_test:] # 測試集索引


# 訓練集
t_u_train = t_u[train_indics]
t_c_train = t_c[train_indics]
# 測試集
t_u_test = t_u[test_indics]
t_c_test = t_c[test_indics]


# 歸一化
t_u_mean = t_u_train.mean()
t_u_std = t_u_train.std()


t_u_train_norm = (t_u_train - t_u_mean) / t_u_std
t_u_test_norm = (t_u_test - t_u_mean) / t_u_std


t_c_mean = t_c_train.mean()
t_c_std = t_c_train.std()


t_c_train_norm = (t_c_train - t_c_mean) / t_c_std
t_c_test_norm = (t_c_test - t_c_mean) / t_c_std


# 2. 搭建模型
import torch.nn as nn


linear_model = nn.Linear(in_features = 1, out_features = 1) # in_features 表示輸入神經元的個數，out_features 表示輸出神經元的個數


# 3. 宣告優化器和損失函數
optimizer = torch.optim.SGD(
    linear_model.parameters(),
    lr=1e-2
)


def loss_fn(t_p, t_c):
    return ((t_p - t_c) ** 2).mean()


# 4. 宣告 train loop
def train_loop(n_epochs, optimizer, model, loss_fun, t_u_train, t_u_test, t_c_train, t_c_test):
    for epoch in range(1, n_epochs + 1):
        t_p_train = model(t_u_train)
        loss_train = loss_fun(t_p_train, t_c_train)


        t_p_test = model(t_u_test)
        loss_test = loss_fun(t_p_test, t_c_test)


        optimizer.zero_grad()
        loss_train.backward()
        optimizer.step()


        if epoch == 1 or epoch % 1000 == 0:
            print(f'Epoch {epoch}: Training Loss: {loss_train:.4f}')
            print(f'Test Loss: {loss_test:.4f}')


# 5. 開始訓練
train_loop(
    n_epochs = 3000,
    optimizer = optimizer,
    model = linear_model,
    loss_fun = loss_fn,
    t_u_train = t_u_train_norm,
    t_u_test = t_u_test_norm,
    t_c_train = t_c_train_norm,
    t_c_test = t_c_test_norm
)

真正的神經網路搭建

不知道讀者讀到這裡，會不會同我一樣，陡然驚醒。我們在之前的例子中，似乎用到的並不是一種可以被稱作“深度學習”的方法。我們只是做了一個線性回歸，並且透過一些深度學習的優化演算法對這個模型進行調優。但無論如何，線性模型就是線性模型，它永遠無法達到神經網路模型的能力。

接下來，我們來搭建一個真正的神經網路模型，用這把鋒利的殺牛刀，來宰殺我們這只小小的問題雞。

其實很簡單，我們上面有說過，一個神經元就是一個線性變換 + 一個激勵函數，一個神經網路是多個神經元的組合。或許只需要將我們的線性模型替換為一個多層的神經網路模型即可。在 PyTorch 中，torch.nn.Sequential 幫助我們將不同的模型做串聯。因此可以使用它來構建一個多層的神經網路。

# 2. 搭建模型
import torch.nn as nn
from collections import OrderedDict


# 構建一個多層神經網路，隱藏層有 13 個神經元，輸出層有 1 個神經元
neural_network = nn.Sequential(OrderedDict([
    ('hidden', nn.Linear(1, 13)), # 隱藏層
    ('hidden_activation', nn.Tanh()), # 隱藏層激勵函數
    ('output', nn.Linear(13, 1)) # 輸出層
]))

然後將訓練參數改成這個模型，訓練完成後我們就可以使用模型預測了。

# 預測
print('output', neural_network(t_u_test_norm) * t_c_std + t_c_mean) # 這裡需要反標準化
print('val', t_c_test)

使用神經網路區分小鳥和飛機

這裡我們使用一個經典的數據集 CIFAR-10 來訓練一個神經網路模型，來區分小鳥和飛機。CIFAR-10 是一個包含 10 個類別的圖像數據集，每個類別有 6000 張圖像，總共有 60000 張圖像。這個數據集包含了小鳥、飛機、汽車、貓、鹿、狗、青蛙、馬、船和卡車等 10 個類別。

我們首先來下載資料集：

import torchvision


# 下載 CIFAR-10 資料集
train_dataset = torchvision.datasets.CIFAR10(
    root='./data',
    train=True, # 訓練集
    download=True
)


test_dataset = torchvision.datasets.CIFAR10(
    root='./data',
    train=False, # 測試集
    download=True
)

我們透過 type(train_dataset).__mro__ 可以看到 train_dataset 是一個 torchvision.datasets.cifar.CIFAR10 的類型，這個類型繼承了 torch.utils.data.Dataset。

Dataset 型別

torch.utils.data.Dataset 是 PyTorch 中的一個抽象類別，用來表示數據集。我們可以透過繼承這個類別，來製作自己的數據集。

torch.utils.data.Dataset 有兩個重要的方法，__len__ 和 __getitem__。__len__ 方法返回數據集的大小，__getitem__ 方法返回一個樣本。如果要繼承這個類別，我們必須要實現這兩個方法。

import torch


class MyDataset(torch.utils.data.Dataset):
    def __init__(self, data):
        self.data = data


    def __len__(self):
        return len(self.data)


    def __getitem__(self, idx):
        return self.data[idx]

DataLoader 型別

torch.utils.data.DataLoader 是 PyTorch 中的一個類別，用來將數據集轉換為可迭代的對象。我們可以通過設置 batch_size、shuffle、num_workers 等參數，來對數據集進行分批、隨機化、多進程加速等操作。

import torch


data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]


dataset = MyDataset(data)


dataloader = torch.utils.data.DataLoader(
    dataset,
    batch_size=2,
    shuffle=True,
    num_workers=2
) # batch_size 表示每個 batch 的大小，shuffle 表示是否隨機化，num_workers 表示多進程加速

資料的準備和歸一化

在訓練神經網路之前，我們需要對數據進行一些預處理，比如將圖像轉換為 Tensor，並且對圖像進行歸一化處理。

import torchvision
import torchvision.transforms as transforms


transforms = transforms.Compose([
    transforms.ToTensor(), # 將圖像轉換為 Tensor
    transforms.Normalize((0.4915, 0.4823, 0.4468), (0.2470, 0.2435, 0.2616)) # 歸一化，第一個 tuple 代表 CIFAR-10 這個資料集 RGB 三個通道的平均值，第二個 tuple 代表標準差
])


train_dataset = torchvision.datasets.CIFAR10(
    root='./data',
    train=True,
    download=True,
    transform=transforms
)


test_dataset = torchvision.datasets.CIFAR10(
    root='./data',
    train=False,
    download=True,
    transform=transforms
)


train_dataloader = torch.utils.data.DataLoader(
    train_dataset,
    batch_size=64,
    shuffle=True,
    num_workers=2
)


test_dataloader = torch.utils.data.DataLoader(
    test_dataset,
    batch_size=64,
    shuffle=False,
    num_workers=2
)

Softmax 方法

Softmax 方法是一個常用的分類方法，它將神經網路的輸出轉換為概率分佈。它不像 Hardmax，把概率高的那個值變成 1，其他變成 0，而是將所有的值都變成 0 到 1 之間的值，並且總和為 1。

Softmax 方法的公式如下：

P(y=i∣x)=exi∑jexjP(y = i | x) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}

Softmax 方法有明顯的“馬太效應”，即強者更強，弱者更弱。這樣，當我們的神經網路訓練好之後，它的預測結果會更加自信，這樣我們就可以更加自信地進行分類。

損失函數

我們使用交叉熵損失函數來衡量模型的預測結果和真實結果之間的差距。交叉熵損失函數的公式如下：

H(y,y^)=−∑iyilog⁡(y^i)H(y, \hat{y}) = -\sum_{i} y_i \log(\hat{y}_i)

在 Python 中，實現交叉商損失函數的方法如下：

import torch.nn.functional as F


def loss_fn(outputs, targets):
    return F.cross_entropy(outputs, targets)

全連結神經網路實現圖像分類

首先，我們為我們的神經網路模型構建資料集。由於我們需要的是將小鳥和飛機進行分類，因此我們只需要 CIFAR-10 中（注：下面的程式碼是直接抄來的，我這一輩子都寫不出這樣簡潔、抽象的程式碼）的第 0 列和第 2 列。

# 構建 label_map，將小鳥和飛機的 label 映射為 0 和 1
label_map = {
    0: 0, # 飛機
    2: 1 # 小鳥
}


# 構建標籤名稱
class_names = ['airplane', 'bird']


# 構建資料集
train_dataset = [(img, label_map[label]) for img, label in train_dataset if label in [0, 2]]
# 最後得到的結果會是一個 list，每個元素是一個 tuple，第一個元素是圖像，第二個元素是 1 或者 2


test_dataset = [(img, label_map[label]) for img, label in test_dataset if label in [0, 2]]


# 構建 DataLoader
train_dataloader = torch.utils.data.DataLoader(
    train_dataset,
    batch_size=64,
    shuffle=True,
    num_workers=2
)


test_dataloader = torch.utils.data.DataLoader(
    test_dataset,
    batch_size=64,
    shuffle=False,
    num_workers=2
)

這裡需要注意，DataLoader 的輸入按道理應該是一個 Dataset，但是我們這裡直接將 Dataset 轉換為了 list 輸入 DataLoader，儘管會有警告，但不會影響運行。

如果你同我一樣是一個強迫症，可以自己實現一個 Dataset 類，然後將這個類傳入 DataLoader。

class MyDataset(torch.utils.data.Dataset):
    def __init__(self, data):
        self.data = data


    def __len__(self):
        return len(self.data)


    def __getitem__(self, idx):
        return self.data[idx]


train_dataset = MyDataset(train_dataset)
test_dataset = MyDataset(test_dataset)

接下來我們構建我們的神經網路模型。這裡我們使用一個全連結神經網路模型，這個模型有一個隱藏層，每個隱藏層有 512 個神經元。

import torch.nn as nn


model = nn.Sequential(
    nn.Linear(32 * 32 * 3, 512), # 輸入層
    nn.Tanh(), # 激勵函數
    nn.Linear(512, 2) # 輸出層
    nn.Softmax(dim=1) # 輸出層激勵函數
)

我們發現，在上面的模型中，我們的輸入層神經元個數是 32 * 32 * 3，這是因為 CIFAR-10 的圖像大小是 32 * 32，並且有 3 個通道（RGB）。發現了嗎？我們相當於把一張圖像的三個維度拉到了一個維度，因此才有了 32 * 32 * 3。我們接下來來做這件事情。

img_batch = img.view(batch_size, -1)

由於 DataLoader 中的資料本身就已經有了 batch_size 的維度，因此我們只需要將圖像的三個維度拉到一個維度即可，並不需要 unsqueeze 升維。

接下來，我們來訓練我們的神經網路模型。這裡我們使用交叉熵損失函數和隨機梯度下降法來訓練模型。

import torch.optim as optim


optimizer = optim.SGD(model.parameters(), lr=1e-2)
loss_fn = nn.NLLLoss()


def train(epoch):
    global loss
    print(len(train_loader))
    for epoch in range(epoch):
        for (image, label) in train_loader:
            batch_size = image.size(0)
            label_batch = torch.tensor(label.detach())


            outputs = model(image.view(batch_size, -1))
            loss = loss_fn(outputs, label_batch)


            optimizer.zero_grad()
            loss.backward()
            optimizer.step()


        print(f"Epoch {epoch}, Loss {loss.item()}")

開始訓練：

train_loop(
    epochs=100,
)

訓練完成後我們使用測試集來測試模型的準確率：

def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for (image, label) in test_loader:
            batch_size = image.size(0)
            label_batch = torch.tensor(label.detach())


            outputs = model(image.view(batch_size, -1))
            _, predicted = torch.max(outputs, dim=1)
            total += label_batch.size(0)
            correct += (predicted == label_batch).sum().item()


    print(f"Accuracy: {correct / total}")

開始使用 CNN

在上面的例子中，我們使用了一個全連結神經網路模型來進行圖像分類。但是，全連結神經網路模型有一個很大的缺點，就是它對圖像的空間信息進行了拉伸，這樣會導致模型對圖像的空間信息的利用不夠充分。

而且我們這還只是一個 32 * 32 的小圖像，如果是一個更大的圖像，那麼全連結神經網路模型就會變得非常龐大，參數量暴增，訓練起來非常困難。

因此，我們需要一種新的神經網路模型，這就是卷積神經網路模型（CNN）。CNN 可以很好地利用圖像的空間信息，並且可以減少參數量，提高模型的訓練速度。

關於 CNN，我們這裡不再贅述，歡迎參閱我之前的文章《機器學習 A-Z 學習筆記（超長文預警）》。

接下來，我們來構建一個 CNN 模型，並且使用這個模型來進行圖像分類。

import torch.nn as nn


conv = nn.Sequential(
    nn.Conv2d(3, 16, kernel_size=3, padding=1), # 卷積層，3 個通道，16 個卷積核，卷積核大小 3 * 3，邊緣為 1
    nn.ReLU(), # 激勵函數
    nn.MaxPool2d(2) # 池化層，2 表示池化核大小
)


model = nn.Sequential(
    conv,
    nn.Flatten(), # 將圖像拉平
    nn.Linear(16 * 16 * 16, 2), # 全連接層
    nn.Softmax(dim=1) # 輸出層激勵函數
)

好，我們現在將我們的模型宣告寫在一個 class 中：

import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):
    def __init__(self):
        super().__init__()


        self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
        self.conv2 = nn.Conv2d(16, 8, kernel_size=3, padding=1)


        self.fc1 = nn.Linear(8 * 8 * 8, 32)
        self.fc2 = nn.Linear(32, 2)


    def forward(self, x):
        out = F.max_pool2d(torch.relu(self.conv1(x)))
        out = F.max_pool2d(torch.relu(self.conv2(out)))
        out = out.view(-1, 8 * 8 * 8)
        out = torch.relu(self.fc1(out))
        out = self.fc2(out)
        return out

然後我們來訓練我們的模型：

import torch.optim as optim


model = Net()


optimizer = optim.SGD(model.parameters(), lr=1e-2)


def train(epoch):
    global loss
    print(len(train_loader))
    for epoch in range(epoch):
        for (image, label) in train_loader:
            batch_size = image.size(0)
            label_batch = torch.tensor(label.detach())


            outputs = model(image)
            loss = loss_fn(outputs, label_batch)


            optimizer.zero_grad()
            loss.backward()
            optimizer.step()


        print(f"Epoch {epoch}, Loss {loss.item()}")

訓練完成後，使用測試集完成測試，發現模型預測準確率在 88% 左右，說明模型訓練效果還不錯，我們可以儲存模型了。

torch.save(model.state_dict(), 'model.pt')

等到下次使用模型時，我們可以這樣載入模型：

model = Net()


model.load_state_dict(torch.load('model.pt'))

換到 GPU 上訓練

在訓練神經網路模型時，我們可以將模型放到 GPU 上進行訓練，這樣可以大大提高訓練速度。

首先我們使用 GPU：

import torch


device = torch.device('cuda' if torch.cuda.is_available() else 'mps' if torch.mps.is_available() else 'cpu')

很多教學寫到 cuda 就完了，好像全世界只有 NVIDIA 才配叫 GPU 一樣⋯⋯我果粉第一個不答應！我們 Mac 上的 GPU 也是可以用來做訓練的，名字叫做 Metal Performance Shaders，簡稱 MPS。因此，我們這裡加上了 mps，這樣就可以在 Mac 上使用 GPU 進行訓練了。

然後我們將模型放到 GPU 上：

model = Net().to(device)

接下來我們將圖像和標籤放到 GPU 上：

image = image.to(device)
label = label.to(device)

這裡筆者在開發的時候有踩一個坑，即將圖像和標籤放到 GPU 上時，需要將 image.to(device) 的結果重新交給 image，否則 image 並不會發生變化，會回報 RuntimeError: Mismatched Tensor types in NNPack convolutionOutput 的 Error。

筆者經過測試，在筆者這台 M3Pro 的 MacBook Pro 上，使用 GPU 訓練速度比 CPU 快了 10 倍左右，這個速度提升是非常可觀的。

模型優化

在訓練神經網路模型時，我們可以使用一些技巧來提高模型的準確率，比如學習率的調整、正則化、Dropout 等。

超參數

調整超參數是一種提高模型準確率的方法，比如，我們可以使用更多的卷積核、更多的隱藏層神經元等（提高寬度），或者增加卷積核的大小、增加隱藏層的層數等（提高深度）。

正則化

正則化是一種防止過擬合的方法，它通過在損失函數中添加一個正則項，來限制模型的複雜度。常見的正則化方法有 L1 正則化和 L2 正則化。

def train(epoch):
    global loss
    for epoch in range(epoch):
        for (image, label) in train_loader:
            image = image.to(device)
            label = label.to(device)
            outputs = model(image)
            loss = loss_fn(outputs, label)


            # L2 正則化
            l2_lambda = 0.001
            l2_norm = sum(p.pow(2.0).sum() for p in model.parameters())
            loss = loss + l2_lambda * l2_norm


            optimizer.zero_grad()
            loss.backward()
            optimizer.step()


        print(f"Epoch {epoch}, Loss {loss}")

Dropout

Dropout 是一種防止過擬合的方法，它通過在訓練過程中隨機丟棄一些神經元，來防止模型對訓練數據的過度擬合。

class Net(nn.Module):
    def __init__(self):
        super().__init__()


        self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
        self.conv2 = nn.Conv2d(16, 8, kernel_size=3, padding=1)


        self.fc1 = nn.Linear(8 * 8 * 8, 32)
        self.fc2 = nn.Linear(32, 2)


    def forward(self, x):
        out = F.max_pool2d(torch.relu(self.conv1(x)))
        out = F.max_pool2d(torch.relu(self.conv2(out)))
        out = out.view(-1, 8 * 8 * 8)
        out = torch.relu(self.fc1(out))
        # Dropout
        out = F.dropout(out, p=0.5, training=self.training)
        out = self.fc2(out)
        return out

ResNet

ResNet 是一種非常流行的神經網路模型，它通過殘差塊（Residual Block）來解決梯度消失的問題，進而實現更深的神經網路。

class ResidualBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride=1):
        super(ResidualBlock, self).__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False)
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(out_channels)
        self.downsample = nn.Sequential()
        if stride != 1 or in_channels != out_channels:
            self.downsample = nn.Sequential(
                nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(out_channels)
            )


    def forward(self, x):
        identity = x
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        out = self.conv2(out)
        out = self.bn2(out)
        out += self.downsample(identity)
        out = self.relu(out)
        return out

僅作了解！之後若有應用，隨用隨查即可。

最後的程式碼

import torch
import torchvision
import torchvision.transforms as transforms
from torch import optim
from torch.utils.data import Dataset
import torch.nn as nn
import torch.nn.functional as F


data_path = "data/"


device = torch.device("cuda" if torch.cuda.is_available() else "mps" if torch.mps.is_available() else "cpu")


transforms = transforms.Compose([
    transforms.ToTensor(),  # 將圖像轉換為 Tensor
    transforms.Normalize((0.4915, 0.4823, 0.4468), (0.2470, 0.2435, 0.2616))
    # 歸一化，第一個 tuple 代表 CIFAR-10 這個資料集 RGB 三個通道的平均值，第二個 tuple 代表標準差
])


train_dataset = torchvision.datasets.CIFAR10(
    root=data_path,
    train=True,
    download=True,
    transform=transforms
)


test_dataset = torchvision.datasets.CIFAR10(
    root=data_path,
    train=False,
    download=True,
    transform=transforms
)


label_map = {
    0: 0,  # 飛機
    2: 1,  # 小鳥
}


class_names = ["airplane", "bird"]


train_dataset = [(img, label_map[label]) for img, label in train_dataset if label in [0, 2]]
test_dataset = [(img, label_map[label]) for img, label in test_dataset if label in [0, 2]]




class ModelDataset(Dataset):
    def __init__(self, dataset):
        self.dataset = dataset


    def __getitem__(self, index):
        img, label = self.dataset[index]
        return img, label


    def __len__(self):
        return len(self.dataset)




train_dataset = ModelDataset(train_dataset)
test_dataset = ModelDataset(test_dataset)


train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=64, shuffle=True)


# 宣告模型
class Net(nn.Module):
    def __init__(self, n_chansl=16):
        super().__init__()


        self.n_chansl = n_chansl


        self.conv1 = nn.Conv2d(3, n_chansl, kernel_size=3, padding=1)
        self.conv1_batchnorm = nn.BatchNorm2d(n_chansl) # 歸一化器，輸入為通道數，輸出為相同的通道數
        self.conv2 = nn.Conv2d(n_chansl, n_chansl // 2, kernel_size=3, padding=1)
        self.conv2_batchnorm = nn.BatchNorm2d(n_chansl // 2)


        self.fc1 = nn.Linear(8 * 8 * n_chansl // 2, 32)
        self.fc2 = nn.Linear(32, 2)


    def forward(self, x):
        out = F.max_pool2d(self.conv1_batchnorm(torch.relu(self.conv1(x))), kernel_size=2)
        out = F.max_pool2d(self.conv2_batchnorm(torch.relu(self.conv2(out))), kernel_size=2)
        out = out.view(-1, 8 * 8 * self.n_chansl // 2)
        out = torch.relu(self.fc1(out))
        out = self.fc2(out)
        return out


model = Net().to(device)


optimizer = optim.SGD(model.parameters(), lr=1e-2)
loss_fn = nn.CrossEntropyLoss()


def train(epoch):
    global loss
    for epoch in range(epoch):
        for (image, label) in train_loader:
            image = image.to(device)
            label = label.to(device)
            outputs = model(image)
            loss = loss_fn(outputs, label)


            l2_lambda = 0.001
            l2_norm = sum(p.pow(2.0).sum() for p in model.parameters())
            loss = loss + l2_lambda * l2_norm


            optimizer.zero_grad()
            loss.backward()
            optimizer.step()


        print(f"Epoch {epoch}, Loss {loss}")




train(100)




def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for (image, label) in test_loader:
            image = image.to(device)
            label = label.to(device)
            outputs = model(image)
            _, predicted = torch.max(outputs, dim=1)
            total += label.size(0)
            correct += (predicted == label).sum().item()


    print(f"Accuracy: {correct / total}")




test()


# torch.save(model.state_dict(), "model/model.pt")

結束了嗎？

這篇文章就算深度學習（神經網路）正是入門了。一路跟著敲下來，筆者算是初步理解了神經網路在 PyTorch 中的實現方案。

之前邵老闆恐嚇我，說 PyTorch 2.0 相對於 PyTorch 1.0 的不相容性有多大，一度讓我心生退意。但是，當我真正開始寫這篇文章的時候，我發現 PyTorch 2.0 和 PyTorch 1.0 的不同並沒有那麼大，甚至不算 Breaking Change。（當然我還是個剛剛入門的小白，大佬不要和我一般見識啦）

我們這篇文章用兩個案例入門了神經網路，但這遠遠不夠。“深度學習”這個坑的“深度”可不算淺。筆者作為一位醫科生，也無法給出這些演算法背後的數學道理。但是，我們可以通過不斷的實踐，來加深我們對這些演算法的理解。笨鳥先飛、熟能生巧，這是學習任何事情的必經之路。

接下來，筆者 AI 方面的文章將會主要涉及到筆者的專業方向，比如影像組學，非本專業的讀者可以參考，但應該與你的領域沒有多少相關性了。

感謝你讀到這裡，我們來日方長，下篇文章再見。

[深度學習] 從幾個示例系統學習 PyTorch 的應用（超長文預警）
https://blog.kynix.tw/posts/1730160669082/
作者
Adrian Chen
建檔時間
2024 年 10 月 29 日
協議
BY-NC-SA 4.0
姓名標示-非商業性-相同方式分享 4.0 國際
© 2025 Adrian Chen
Powered by Astro