統計學（1）

開一個新的文章集合，是我學習統計學的隨課筆記，可以看作我上一個集合《R Lang與高級醫學統計學》的統計學部分。我學習統計學的資料來自於國立陽明交通大學的公開課程（NYCU OCW）的《統計學》課程，授課教師是唐麗英博士。你可以在 YouTube 或者 NYCU OCW 的官方網站（https://ocw.nycu.edu.tw）上面找到這門課。

基本統計專有名詞

1. 群體（population）：由具有共同特性之個體所組成的整體。
2. 樣本（sample）：群體之一部分。
3. 參數（parameter）：由群體資料所計算之群體表徵值。
   • 群體平均數：$\mu$
   • 群體標準差：$\sigma$
   • 群體比例：$p$
4. 統計量（statistic）：由樣本資料所計算之樣本表徵值。
   • 樣本平均數：$\overline{x}$
   • 樣本標準差：s
   • 樣本比例：$\hat{p}$
5. 隨機變數（Random Variable, R.V.）：研究者對所欲研究問題定義之群體所感興趣的一項或多項特質，稱為隨機變數。觀察各項隨機變數之結果稱為資料（data）。
6. 實驗單位（Experimental Unit）：研究者由所欲研究之人或物上取得隨機變數之量測值，這些人或物稱為實驗單位。

• 統計學的主要目的：由樣本所得資訊推論母體參數。

例子：某製程工程師欲由 100 片隨機抽出之晶圓來估計晶圓之厚度。請指出此例欲研究之群體、樣本、參數、統計量、隨機變數及實驗單位各為何？

• 群體：本批次所有晶圓的厚度。
• 樣本：隨機抽出的 100 片晶圓之厚度。
• 參數：所有晶圓的平均厚度。
• 統計量：隨機抽出的 100 片晶圓之厚度。
• 隨機變數：晶圓的厚度。
• 實驗單位：晶圓。

統計學的範圍

• 敘述統計（Descriptive Statistics）：包含蒐集數據、展示數據及找出可描述數據特徵之值的方法。
• 推論統計（Inferential Statistics）：包含由樣本資訊來推論群體，並估計該推論之可信度大小的方法。

隨機變數的類別

1. 定性變數（Qualitative random variables）：定性變數產生定性資料，即隨機變數的各結果不能以數量表示，而僅能依其特性之類別表之。譬如性別（gcnder）、國籍（Nationality）等。
2. 定量變數（Quantitative random variables）：定量變數產生數值資料，即隨機變數的各結果可以數量表之。
   • 離散型資料（Discrete Random variables）：經由計數的方式取得變數之資料。例如不良品個數、一份文件之錯誤字數、晶圓上之缺陷點數。
   • 連續型變數（Continuous data）：經由量測的方式取得變數資料。例如重量、高度、溫度。

例子：決定下列隨機變數為定性或定量，若為定量則決定其屬離散型或連續型：
a）一片玻璃上之氣泡數。
b）晶圓厚度（Thickness）。
c）一包速食麵之淨重。
d）學生修統計課不及格的原因。

• a：定量-離散型
• b：定量-連續型
• c：定量-連續型
• d：定性

常用的統計圖表

• 類別變數（定性資料）常用圖表：條圖（Bar Graph）、單圓圖（Pie Chart）與柏拉圖（Pareto Diagram）。
• 定量變數（數值資料）常用圖表：莖葉圖（Stem-and-LeafDisplay），直方圖（Histogram）散佈圖（Scatter Diagram）與時間序列圖（Line Charl）。

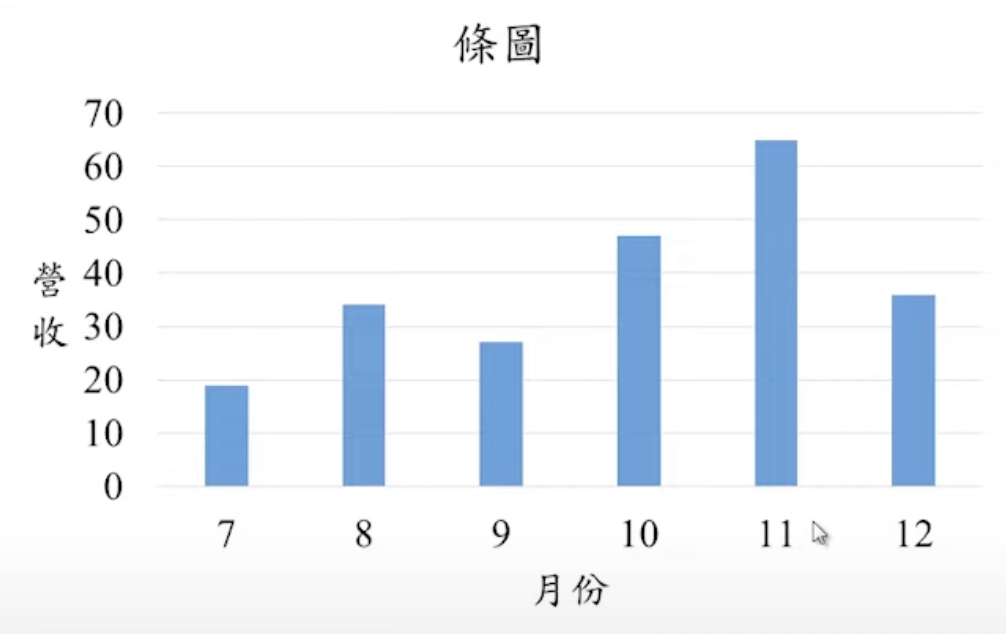
條圖

• 用於比較和對照不同類別或期間的差異。

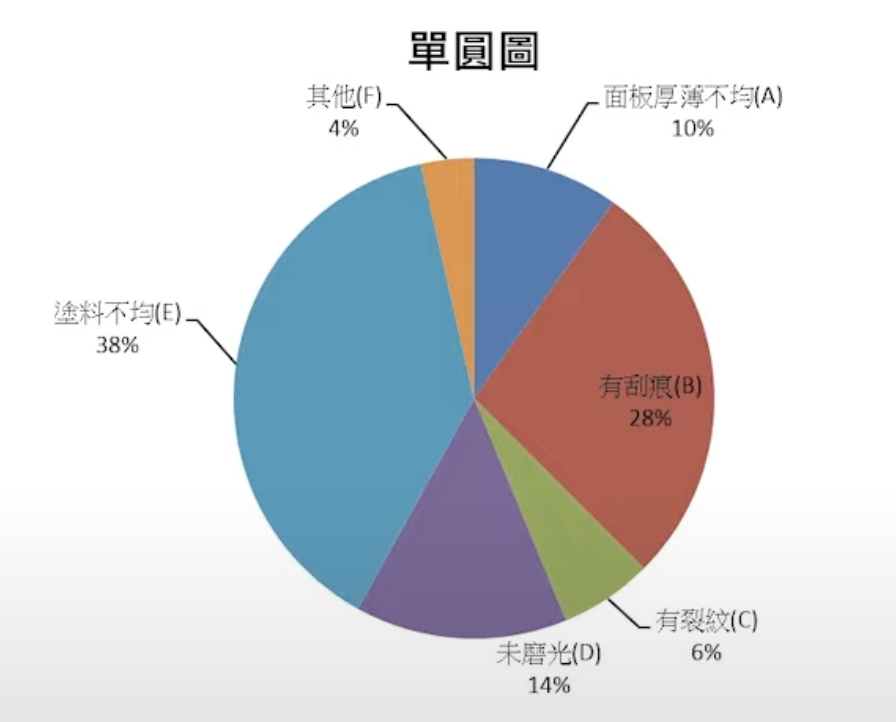
單圓圖

• 主要是用來顯示一個單一總合量如何攤分於各種類別中。

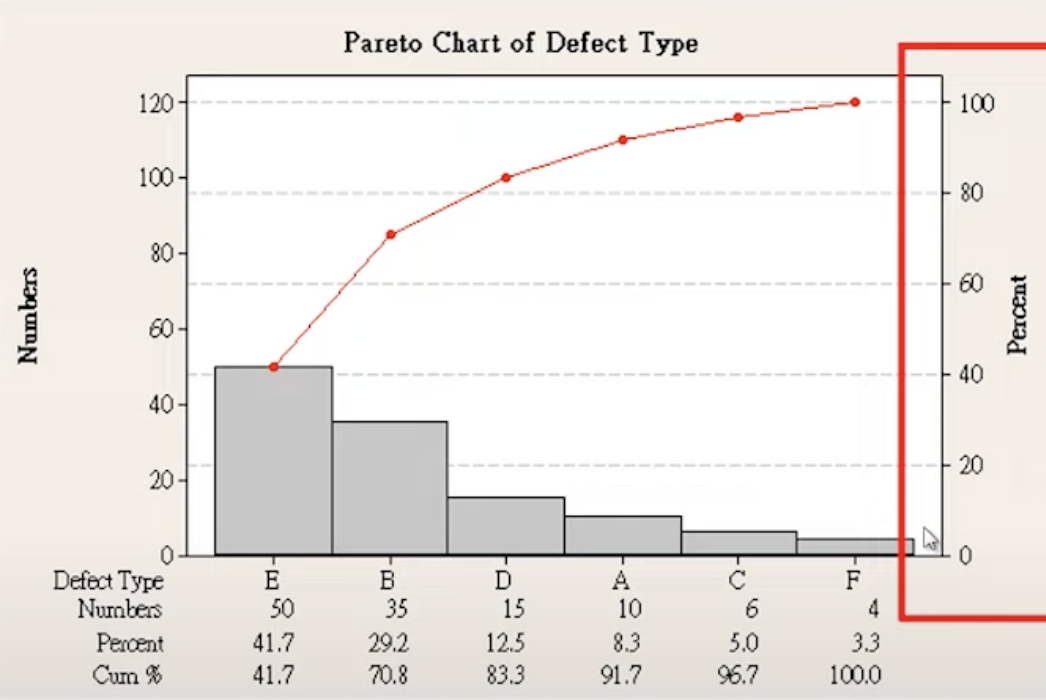
柏拉圖

• 重要少數理論。

莖葉圖

• 用於大量資料的快速排序。
• 每一筆資料的最後一個數字為葉，其餘為莖。

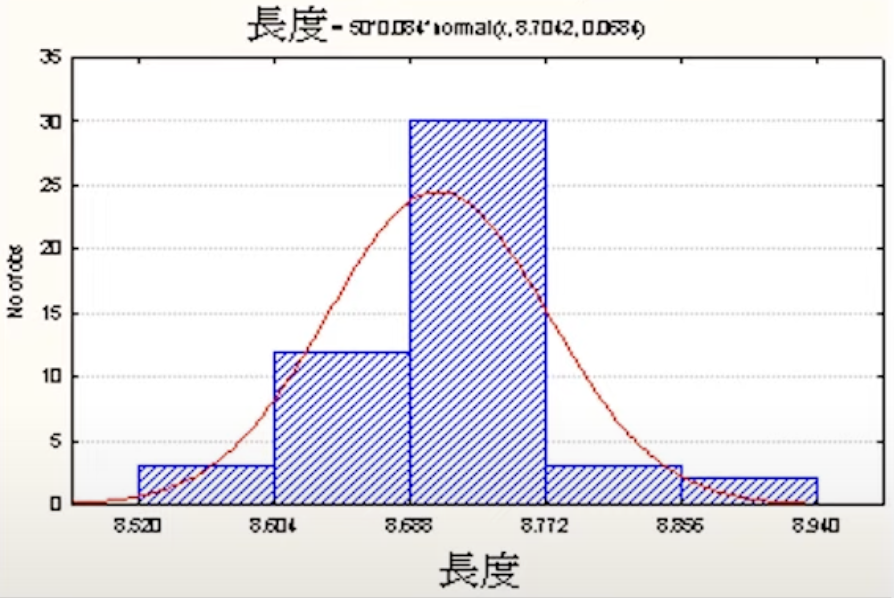
直方圖

• 是連續型資料最常使用的圖形，用來展示資料之分佈。

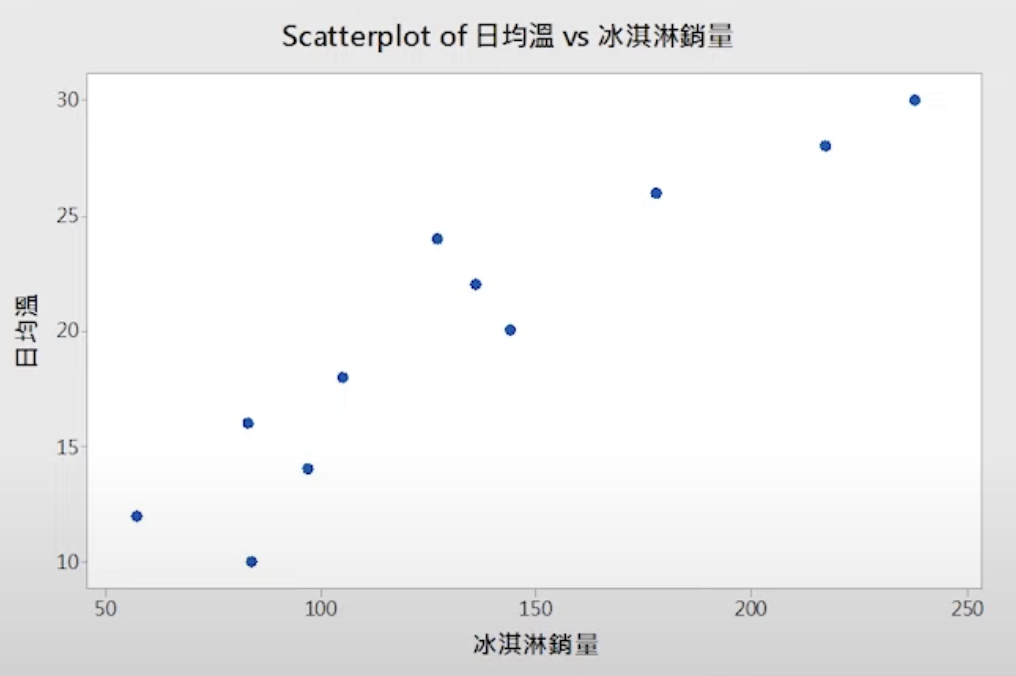
散佈圖

• 散佈圖主要是用來表示資料兩個變數間的關係。

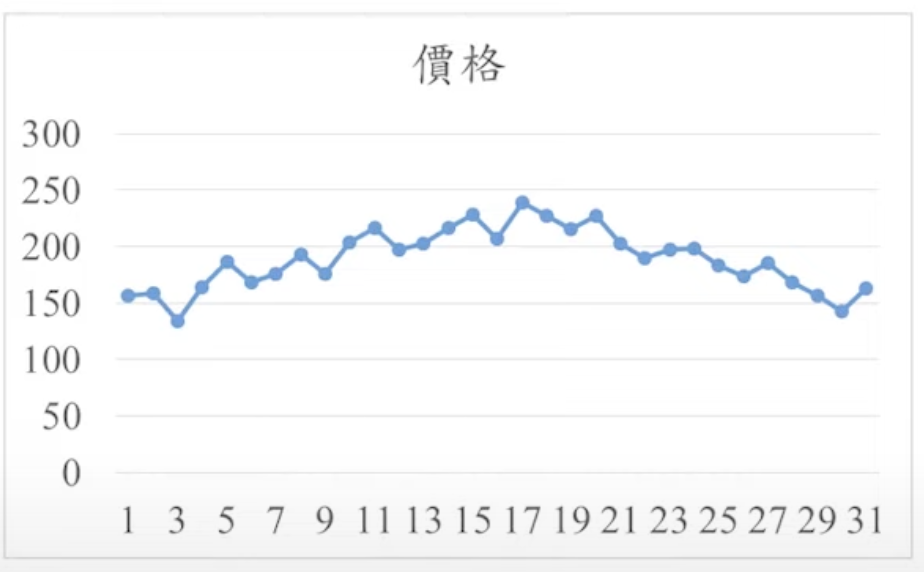
時間序列圖

• 時間序列圖（line chart）是用來表示資料在不同時間的關係圖，通常時間為橫軸，而縱軸則表示觀測值的單位數量。

資料的取得方式

普查

在欲研究之群體中蒐集每一個體之資料，也就是 100% 的全檢。

抽查

利用一種程序或方法，從群體中抽出樣本。

簡單隨機抽樣

• 是指群體中每一個體被抽中之機會均相同。
• 作法：對群體內的每個個體編號，再以亂數表、電腦模擬亂數或製作紙籤的方法決定欲抽取之樣本。
• 優點：取樣方法簡便。
• 缺點：有時會因抽到的樣本過於集中在某部分之群體，而造成樣本之代表性不足。

系統抽樣

• 只做第一次隨機抽樣後，然後依固定間隔數抽出一樣本，直至抽出所欲之樣本數。
• 優點：抽出第一個種子號碼後，僅需每間隔數個樣本抽樣即可，取樣方法簡便。
• 缺點：樣本在編號排序時必須與研究者所關心的變數無關，否則會造成樣本之代表性不足。

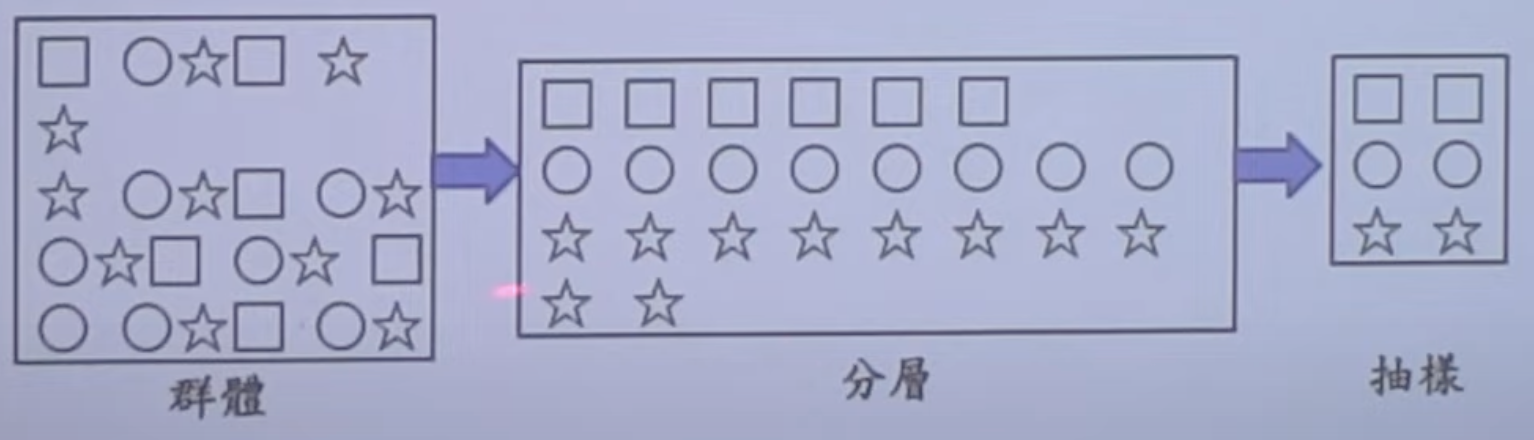
分層隨機抽樣

• 作法：先將群體依某一衡量標準分成數個不重疊的子群（稱為層），再從每一子群（層）中利用簡單隨機方式抽取樣本，即為分層隨機抽樣。
• 分層隨機抽樣之原則是同層內的性質差異要小，而不同層間之差異則要越大越好。

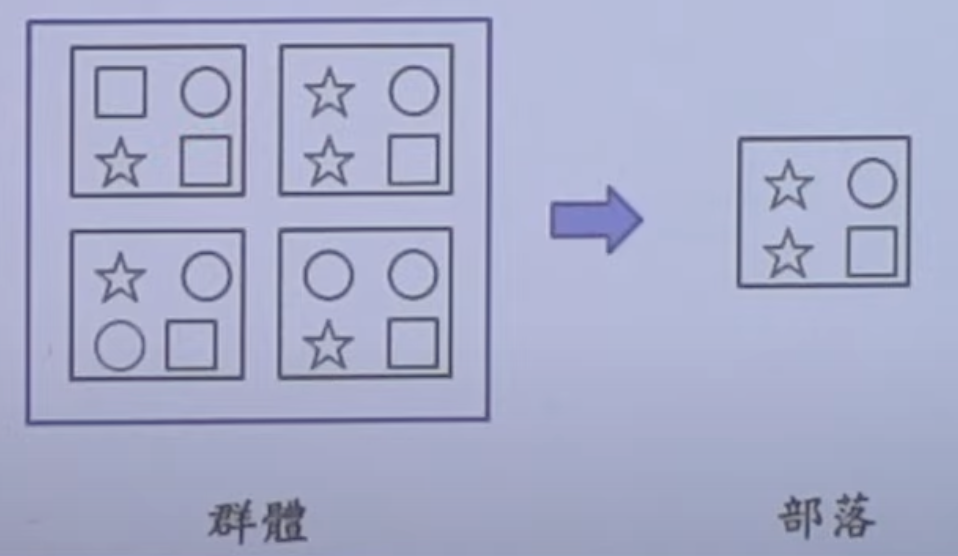
部落抽樣

• 常用在群體中之個體分離相當遠，且很難蒐集到其樣本資料時。
• 作法：部落抽樣先將群體分成數個部落，再從同一個部落中抽出一個或數個部落進行普查。
• 部落抽樣是假設每一個部落都是群體的縮影，因此不同部落間個體性質的差異要小，而同一部落內個體性質的差異性大。