統計學（7）

這篇文章介紹常用之連續型機率分佈。在醫學領域，基本只需要理解幾個比較重要的機率分佈模式即可，或許常態分佈理解就夠了，其他的了解即可。

常態分佈

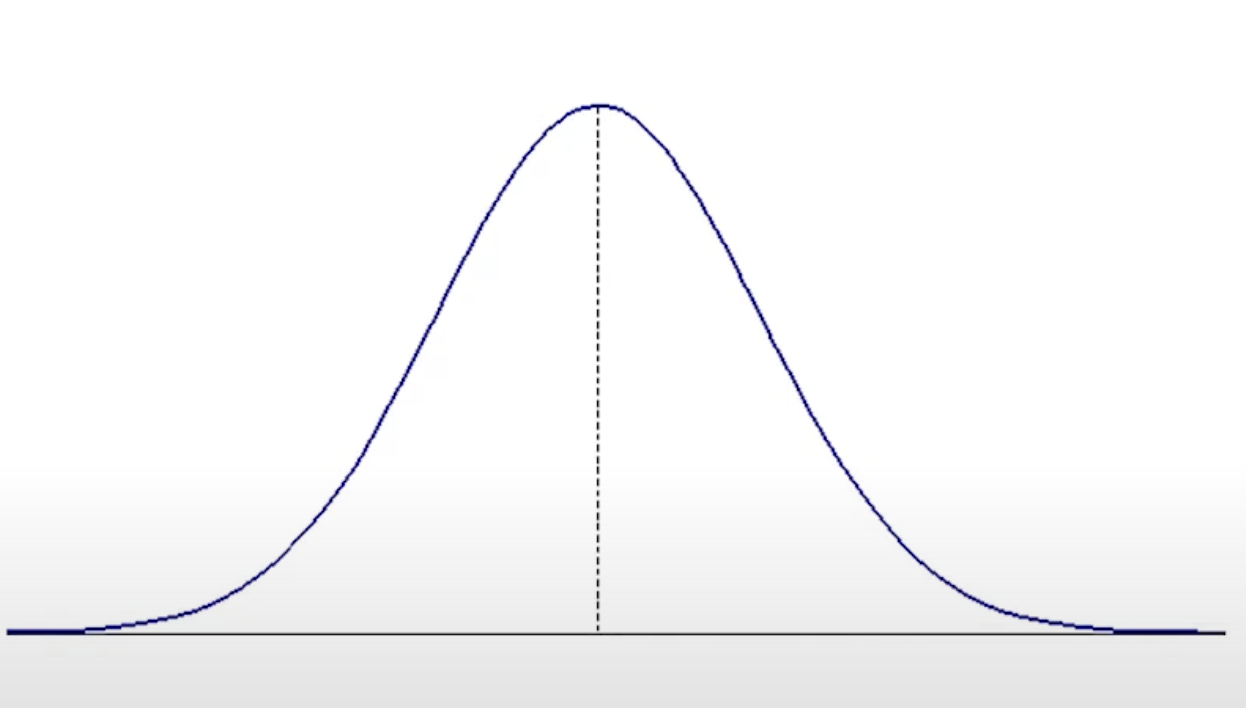
機率密度函式：

$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-(x - \mu)^2/2\sigma^2}, -\infty < x < +\infty$

常以 $N(\mu, \sigma)$ 或者 $N(\mu, \sigma^2)$ 表示。

• $\mu$：影響圖像中心的位置。$\mu$ 越大，曲線中心右移。
• $\sigma$：影響圖像的形狀。$\sigma$ 越大，曲線越矮胖。

特性：

1. 圖像對稱於 $\mu$
2. 隨機變數x的值可由 $-\infty$ 至 $+\infty$
3. 鍾形分佈
4. 曲線下面積為 1
5. 集中趨勢量數（平均數、中位數、眾數相同）

標準常態分佈

$N(0, 1)$ 為標準常態分佈，使用字母 Z 表示。因此標準常態分佈又可以稱為 Z 分佈。

一般常態分佈之標準化：

$Z = \frac{X - \mu}{\sigma}, Z\sim N(0, 1)$

常態分佈的判斷

1. 直方圖：只要出現鐘形分佈圖形，即判定數據呈常態分佈。
2. 常態機率圖：只要圖形接近直線，即判定數據呈常態分佈。
3. 統計假設檢定：只要以下統計檢定之顯著度 $p-value>0.05$，即判定數據呈常態分佈。
   • 卡方適配度檢定
   • K-S 檢定
   • A-D 檢定

使用常態機率估算二項機率

當 n 很大，p 接近 0.5 時，可以使用常態機率來估算二項機率。

例8：擲一個銅板 100 次，試求以下機率：

1. 至少看到 70 次正面（人頭）？
2. 看到正好 50 次正面？

首先做連續性校正。其含義是：如果一個離散型隨機變數 X，有 $P(a \le X \le b)$，則將其 pass 為：$P(a - \frac{1}{2} \le X \le b + \frac{1}{2})$

則上述問題轉化為：

1. $P(X \ge 69.5)$，或 $P(Z = \frac{X - \mu}{\sigma} \ge 3.9)$
2. $P(49.5 \le X \le 50.5)$，或 $P(-0.1 \le Z = \frac{X - \mu}{\sigma} \le 0.1)$

轉化爲 $\mu = np$，$\sigma = \sqrt{npq}$ 之常態分佈。

則 $\mu = 50$，$\sigma = 5$，則有 $X \sim N(50, 5)$。

查表得：

1. $P(X \ge 70) \approx 0.005\%$
2. $P(X = 50) \approx 7.96\%$

對數常態分佈

當變數X之自然對數 $\ln X$ 呈常態分佈，則 X 服從對數常態分佈。

機率密度函數：$f(x) = \begin{cases} \frac{1}{\sqrt{2\pi}\beta}x^{-1}e^{\frac{(\ln x - \alpha)^2}{2\beta^2}}, x > 0,\beta > 0\\ 0, otherwise \end{cases}$

期望值和變異數：

1. 期望值：$Exp(X) = \mu = e^{\alpha + \frac{1}{2}\beta^2}$
2. 變異數：$Var(X) = \sigma^2 = e^{2\alpha + \beta^2(e^{\beta^2} - 1)}$

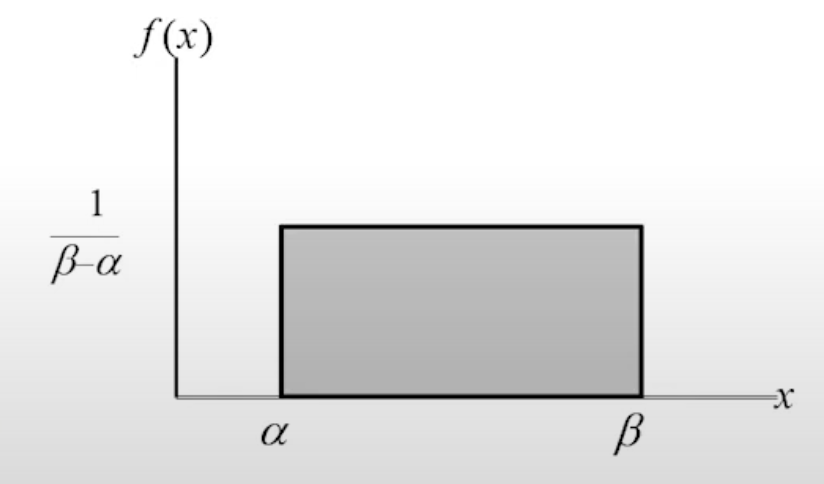
齊一分佈（均等分佈）

連續型隨機變數 X 為齊一隨機變數，則 X 在某一連續的區間上有相同的機率密度。X 之機率密度函數如下：

$f(x) = \begin{cases} \frac{1}{\beta - \alpha}, \alpha < X < \beta\\ 0, otherwise \end{cases}$

期望值：

$Exp(X) = \mu = \frac{\alpha + \beta}{2}$

變異數：

$Var(X) = \sigma^2 = \frac{(\beta - \alpha)^2}{12}$

指數分佈

機率密度函數：

$f(x) = \begin{cases} \lambda e^{-\lambda x}, x > 0, \lambda > 0\\ 0, otherwise \end{cases}$

期望值：

$Exp(X) = \frac{1}{\lambda}$

變異數：

$Var(X) = \frac{1}{\lambda^2}$

累加函數：

$F_X(t) = P(X \le t) = \int_0^t \lambda e^{-\lambda x} dx = 1 - e^{-\lambda t}$

則 $P(X > t) = e^{-\lambda t}$

在波瓦松過程中，兩連續事件間的等候時間呈現指數分佈。

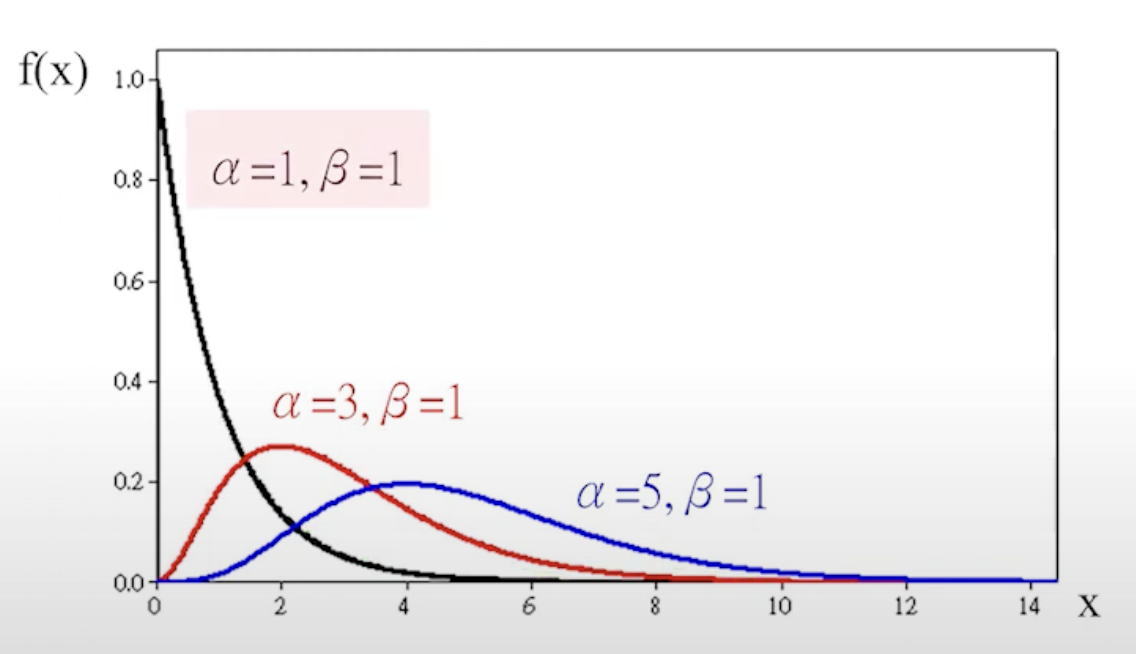
伽馬分佈

機率密度函數：

$f(x) = \begin{cases} \frac{1}{\beta^\alpha \Gamma(\alpha)}x^{\alpha - 1}e^{-\frac{x}{\beta}}, x > 0, \alpha > 0, \beta > 0\\ 0, otherwise \end{cases}$

其中 $\Gamma(x)$ 爲伽馬函數：$\Gamma(x) = \int_0^{\infty} x^{\alpha - 1}e^{-x}dx, \alpha > 0$

伽馬函數的特性：

1. $\Gamma(\alpha) < \infty, if\ \alpha > 0$
2. $\Gamma(\alpha) = (\alpha - 1)\Gamma(\alpha - 1), if\ \alpha > 1$
3. $\Gamma(\alpha) = (\alpha - 1)!$，當 $\alpha$ 爲一正整數

期望值與變異數：

$Exp(X) = \alpha \beta$

變異數：

$Var(X) = \alpha \beta^2$

韋伯分佈

機率密度函數：

$f(x) = \alpha \beta (\beta x)^{\alpha - 1} e^{-\beta x^\alpha}, x > 0$

$\alpha > 0, \beta > 0$，$\alpha$ 爲形狀參數，$\beta$ 爲尺度參數。

當 $\alpha = 1$，韋伯分佈是指數分佈（$\lambda = \frac{1}{\beta}$），$\alpha = 2$ 時，韋伯分佈是瑞利分佈。

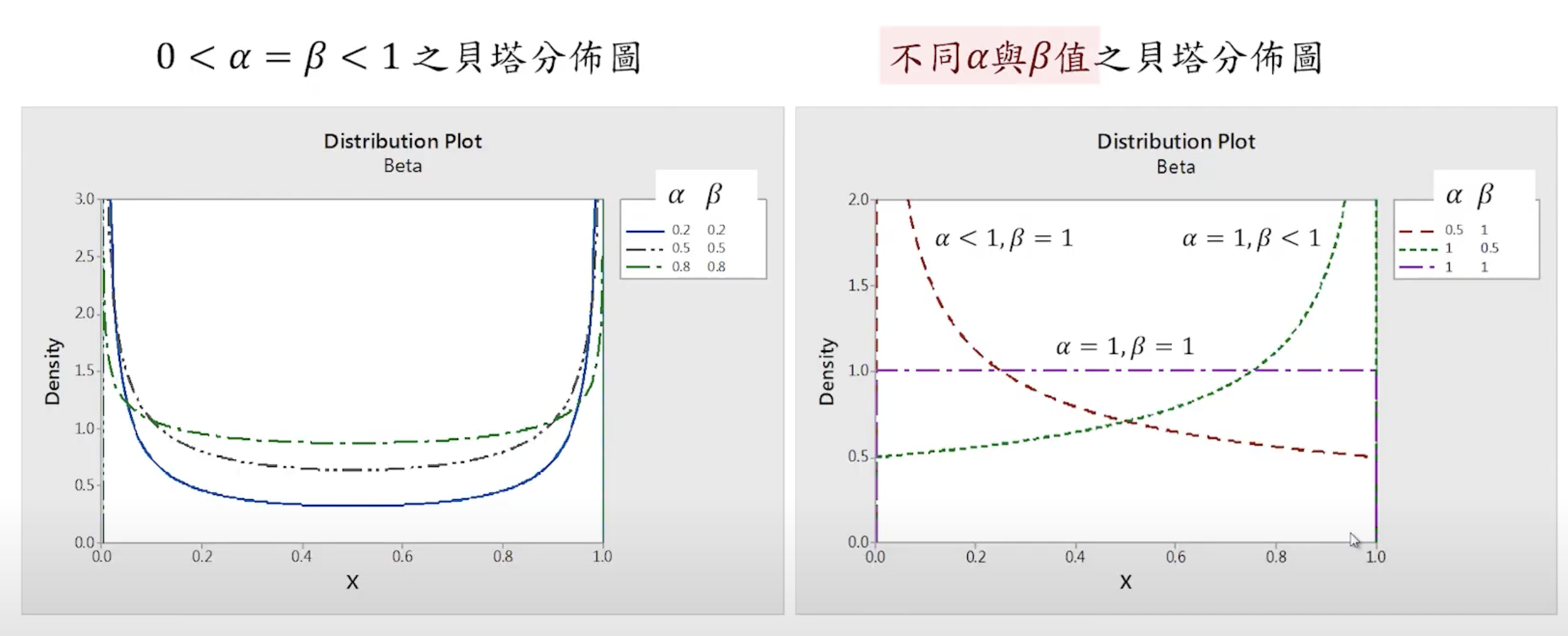
貝塔分佈

機率密度函數：

$f(x;\alpha;\beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha - 1}(1 - x)^{\beta - 1}, 0 < x < 1, \alpha, \beta > 0$