統計學（9）

推理統計實際上是群體的參數未知，使用樣本統計量來推理群體參數的方法。推理統計分為估計和檢定。

這篇文章介紹估計。估計分為點估計和區間估計。

點估計

定義：一個群體參數之點估計式或估計量（estimator）是一個法則（rule）或公式（formula），利用此法則或公式可以由樣本資料中計算出一個單一數值（single number）以估計群體參數。由點估計式所得之單一數值稱為該參數之估計值（estimate）。

例如，$\mu$ 的估計值是 $\overline{X}$，$\sigma$ 的估計值是 $s$，$P$ 的估計值是 $\hat{p}$。

區間估計

定義：一個群體參數之區間估計式（interval estimator）是一個法則（rule），利用此法則可以由樣本資料中計算出兩個數字（two numbers）或一個區間之上、下限以估計群體參數，並指出該區間包含群體參數的機率。

信賴係數：信賴係數（或信賴度）是指區間估計式之上下限，包含群體參數之機率或信心。

信賴區間的意義：我們有 $(1-\alpha)100\%$ 的信心認為統計量會落在計算出的區間內。

$\mu$ 的區間估計

大樣本（large sample）

根據中央極限定理，$\overline{X}$ 服從常態分配：$\overline{X} \sim N(\mu, \sigma/\sqrt{n})$。

$(1-\alpha)100\%$ 的信賴區間：$\overline{X} \pm Z_{\frac{1-\alpha}{2}}\frac{\sigma}{\sqrt{n}}$（$\sigma$ 已知）、$\overline{X} \pm t_{\frac{\alpha}{2}, n - 1}\frac{s}{\sqrt{n}} \approx \overline{X} \pm Z_{\frac{1-\alpha}{2}}\frac{s}{\sqrt{n}}$（$\sigma$ 未知）

$1-\alpha$ 稱信賴係數；$(1-\alpha)\times 100\%$ 稱信賴水準。一般使用 95%。

小樣本（small sample）

前提：群體假定接近常態分配。

$(1-\alpha)100\%$ 的信賴區間：$\overline{X} \pm t_{\frac{\alpha}{2}, n - 1}\frac{s}{\sqrt{n}}$

$P$ 的區間估計

適用於大樣本（$n\hat{p} \ge 4 \&\& n\hat{q} \ge 4$）的 $(1 - \alpha)\times 100\%$ 信賴區間：$\hat{p} \pm Z_{\frac{\alpha}{2}}\sqrt{\frac{\hat{p}\hat{q}}{n}}$

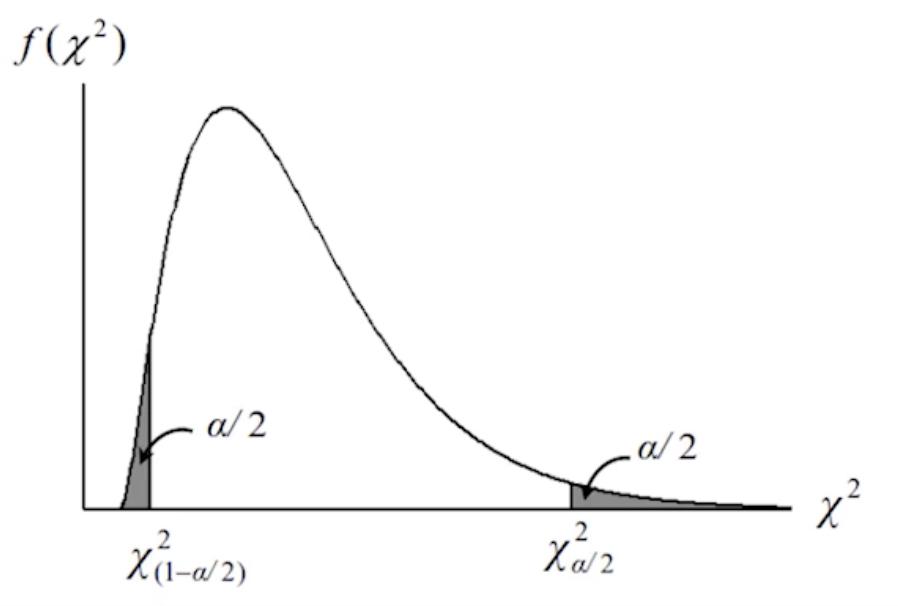
$\sigma^2$ 的區間估計

前提：假定群體服從近似常態分佈。

$(1 - \alpha)100\%$ 信賴區間：$\frac{(n - 1)s^2}{\chi_{\frac{\alpha}{2}}^2} \le \sigma^2 \le \frac{(n - 1)s^2}{\chi_{1 - \frac{\alpha}{2}}^2}$

選擇樣本數以估計群體參數值

$\mu$ 的選擇

我們期望：得到一個樣本數量 n，使得 $\mu$ 的估計值同真實值的誤差不超過E個單位的機率為 $(1-\alpha)$：

$n = \left[ \frac{Z_{(1- \alpha)/2}\sigma}{E} \right]^2$

如果 $\sigma^2$ 未知，則使用 $s^2$ 代替。

P 的選擇

我們期望：得到一個樣本數量 n，使得 P 的估計值同真實值的誤差不超過 E 個單位的機率為 $(1-\alpha)$：

$n = pq\left[ \frac{Z_{(1-\alpha)/2}}{E} \right]^2$

此公式中的 p 和 q 可以使用過去資料來估計。

兩個群體參數差異之區間估計

獨立樣本的平均數差異（$\mu_1 - \mu_2$）區間估計

大樣本：$(\overline{X_1} - \overline{X_2}) \pm Z_{\frac{1-\alpha}{2}} \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}$，如果 $\sigma_1$ 和 $\sigma_2$ 未知，使用 $s$ 代替（t 分佈和 z 分佈接近）。

• 如果 $LCL > 0, UCL > 0$，群體參數 $\theta_1 > \theta_2$
• 如果 $LCL < 0, UCL < 0$，群體參數 $\theta_1 < \theta_2$
• 如果 $LCL < 0, UCL > 0$，群體參數 $\theta_1$和$\theta_2$沒有辦法推論是有差異的。（注意！不是沒有差異，是沒有辦法證明有差異）

小樣本，$\sigma_1$ 和 $\sigma_2$ 均未知，但假定 $\sigma_1 = \sigma_2 = \sigma = s_p = \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2} = \frac{\Sigma_{i = 1}^n (x_{1i} - \overline{X}_1)^2 + \Sigma_{i = 1}^n (x_{2i} - \overline{X}_2)^2}{n_1 + n_2 - 2}$，則有：$(\overline{x_1} - \overline{x_2}) \pm t_{\alpha / 2}\sqrt{s_p^2(\frac{1}{n_1} + \frac{1}{n_2})}, d.f = \nu = n_1 + n_2 - 2$

• $\sigma$ 判斷方法：如果 $\frac{s_1^2}{s_2^2} \le 3$，則一般認為兩個 $\sigma$ 沒有差。

小樣本：$\sigma_1$ 和 $\sigma_2$ 均未知，但 $\sigma_1 \neq \sigma_2$，則有：$(\overline{x_1} - \overline{x_2}) \pm t_{\alpha / 2}\sqrt{\frac{s_1}{n_1} + \frac{s_2}{n_2}}, d.f = \nu = \frac{(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2})^2}{\frac{(\frac{s_1}{n_1})^2}{n_1 - 1} + \frac{(\frac{s_2}{n_2})^2}{n_2 - 1}}$

配對樣本的平均數差異（$\mu_1 - \mu_2$）區間估計

$\mu_1 - \mu_2$ 之 $(1- \alpha)100$ 的信賴區間估計：

大樣本：$\overline{d} \pm Z_\frac{1-\alpha}{2}\left( \frac{\sigma_d}{\sqrt{n}} \right)$

小樣本：$\overline{d} \pm t_\frac{\alpha}{2}\left( \frac{s_d}{\sqrt{n}} \right)$

例：某健身中心針對欲減重者提供減肥運動計畫，並隨機抽取 12 位欲減重者參加此減肥運動計畫。兩個月後量測每位欲減重者之體重（以公斤為單位），減肥前後資料如下表所示。請找出減肥前後體重差異的 95% 信賴區間。請問減肥運動計畫是否有效？

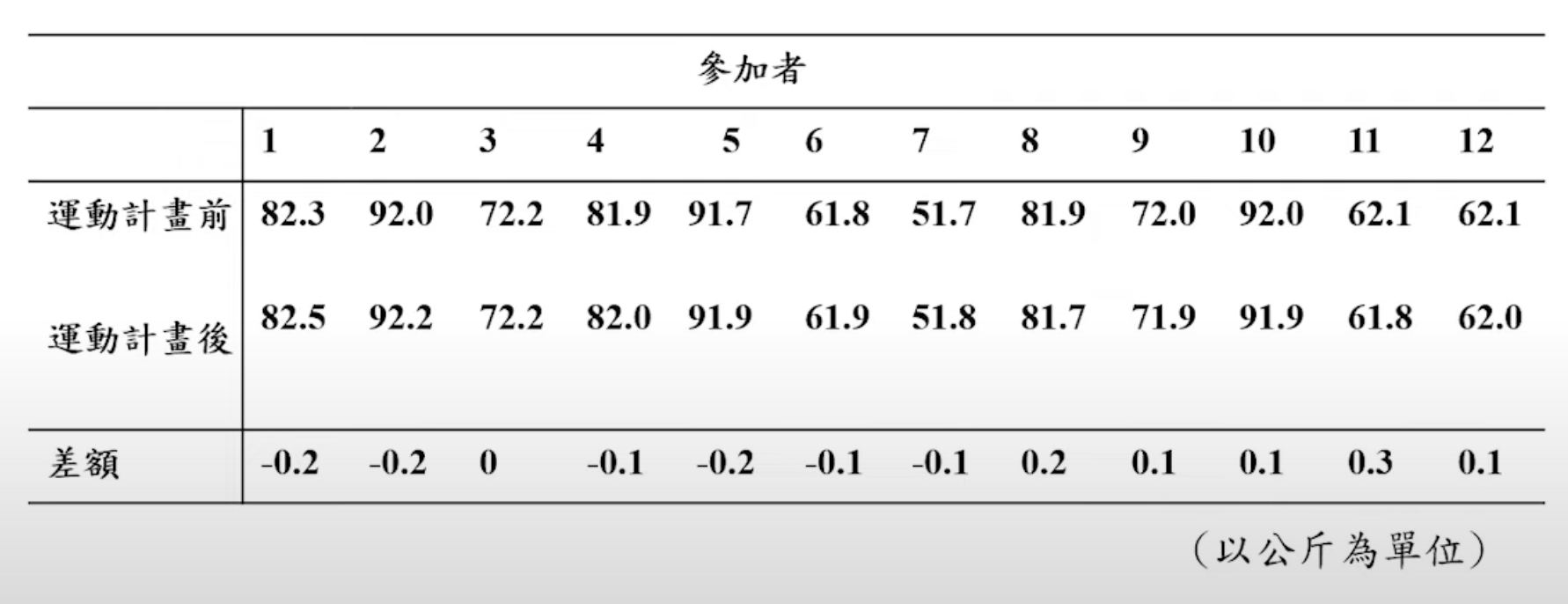
解決如下：

獨立樣本的比例差差異（$P_1 - P_2$）區間估計

條件：大樣本（$n_1\hat{p_1} \ge 4, n_1\hat{q_1} \ge 4, n_2\hat{p_2} \ge 4, n_2\hat{q_2} \ge 4$）

$(\hat{p_1} - \hat{p_2}) \pm Z_{\frac{1-\alpha}{2}}\sqrt{\frac{\hat{p_1}\hat{q_1}}{n_1} + \frac{\hat{p_2}\hat{q_2}}{n_2}}$

獨立樣本的變異數比的差異（$\frac{\sigma_1^2}{\sigma_2^2}$）區間估計

$\frac{s_1^2}{s_2^2}\frac{1}{F_{\alpha / 2(\nu_1, \nu_2)}} \le \frac{\sigma_1^2}{\sigma_2^2} \le \frac{s_1^2}{s_2^2}F_{\alpha/2(\nu_2, \nu_1)}$

選擇樣本大小（n）以估計兩群體參數差異

• $\mu_1 - \mu_2$： $n_1 = n_2 = \left[ \frac{Z_{(1-\alpha)/2}}{E} \right]^2 (\sigma_1^2 + \sigma_2^2)$

• $P_1 - P_2$： $n_1 = n_2 = \left[ \frac{Z_{(1-\alpha)/2}}{E} \right]^2 (p_1q_1 + p_2q_2)$